Toward Quantifying Semiotic
Agencies:
Habits Arising
© This paper is not for reproduction without
permission of the author.
ABSTRACT
Mathematics and Semiotics do not at first seem like a natural couple. Mathematics finds most of its applications describing explicit, mechanical situations, whereas the emphasis in Semiotics is usually toward that which remains at least partially obscure. Nonetheless, probability theory routinely treats circumstances that are either acausal or the results of agencies that remain unknown. Between the domains of the explicitly mechanical and the indescribably stochastic lies the realm of the tacit and the semiotic - what Karl Popper has described as 'a world of propensities.' Popper suggested that some form of Bayesian statistics is appropriate to treat this middle ground, and recent advances in the application of information theory to the description of development in ecosystems appear to satisfy some of Popper’s desiderata. For example, the information- theoretic measure, 'ascendency', calculated upon a network of ecosystem exchanges, appears to quantify the consequences of constraints that remain hidden or only partially visible to an observer. It can be viewed as a prototype of 'quantitative semiotics.' Furthermore, the dynamics consisting of changes in hidden ecosystem constraints do not seem to accord well with the conventional scientific metaphysic, but rather they point towards a new set of postulates, aptly described as an 'ecological metaphysic'.
1 MATHEMATICS AND THE OBSCURE
Semiotics deals with that which is not explicit about the operation of a system -Michael Polyani's realm of the tacit. As such, semiotics does not seem to be a particularly fertile discipline for the mathematician or engineer. For example, Stanley Salthe, who writes elsewhere in SEED, once proclaimed to the author, “If one can put a number on it, it is probably too simplistic to warrant serious discussion!” If, then, the normal objects of semiotic discourse challenge one’s abilities at description, what place could the field possibly hold for mathematical discourse and quantification?
Most probably have read the preceding paragraph in the context of conventional mechanistic, reductionist science, where the usual procedure is first to visualize and describe a mechanism in words before its action is then recast as a mathematical statement. But one need not search far to encounter exceptions to this practice. For example, a random, stochastic assembly of events is amenable to treatment by probability theory, with its powers to quantify that which cannot be described in detail, or even properly visualized. True, the semioticist might reply, but there is little in the wholly stochastic realm to capture one’s interest, for each action is wholly unique, although a summary of individual behavior will occasionally lead to deterministic lawfulness on the part of the ensemble.
The rejoinder by the semioticist would seem to indicate that the proper domain of semiotics appears to occupy some middle ground between the explicit, determinate world of classical science and the indecipherable, nominalist realm of absolute disorder. Forces are out of place in this middle kingdom; events don’t always follow one another without exceptions. Yet even heresome generalizations do seem possible, and some trends are at times observable. As Charles Saunders Peirce cogently observed, 'Nature takes on habits.' (Hoffmeyer 1993.) Now, if mathematical description is effective in the domains that bracket semiotics, there should be no reason to exclude apriori the possibility that some degree of quantification of Peirce’s habits could be achieved - regardless of how hidden their natures might remain. Hence, it is an attempt to quantify at least certain semiotic actions that will occupy the remainder of this essay.
The conventional wisdom holds that all of nature can be portrayed as an admixture of strict mechanism and pure chance, as if the two could be co-joined immediately with each other without thereby excluding anything of interest or importance. Such assumption, however, marginalizes, if not excludes the recognition by the semioticist of the necessity for some middle ground. The semiotic viewpoint seems to be that each of the two current pillars of science (i.e., mechanism and pure chance) seems insufficient and incomplete in ways that cannot be fully complemented by its counterpart. While it is the goal of semiotics to explore and at least partially describe the dynamics of this middle realm, the purpose here is to complement at least some of the resulting narrative by rendering it quantitative and operational - i.e., to write some of semiotic dynamics in numbers.
This task, of course, will necessitate a partial deconstruction of the conventional perspective. It is necessary, therefore, first to enumerate the basic assumptions that support the common view. Towards that end it is useful to construct a strawman that portrays the nature of Newtonian thought at its zenith at the beginning of the Nineteenth Century. While hardly anyone still subscribes to all elements of this metaphysic, most continue to operate as though several of these postulates accord fully with reality. Although much has been written on the scientific method, one rarely finds the fundamental tenets of Newtonian science written out explicitly. One source that attempts to enumerate the assumptions is Depew and Weber (1994), whose list has been emended by Ulanowicz (1999) to include:
(1) Newtonian systems are causally closed. Only mechanical or material causes are legitimate.
(2) Newtonian systems are deterministic. Given precise initial conditions, the future (and past) states of a system can be specified with arbitrary precision.
(3) Physical laws are universal. They apply everywhere, at all times and over all scales.
(4) Newtonian systems are reversible. Laws governing behavior work the same in both temporal directions.
(5) Newtonian systems are atomistic. They are strongly decomposable into stable least units, which can be built up and taken apart again.
2 THE OPEN UNIVERSE
According to the first precept, all events are the conjunctions of relatively few types of simple mechanical events. Seen this way, the same sorts of things happen again and again - phenomena are reproducible and are subject to laboratory investigation in the manner advocated by Francis Bacon. No one can deny that this approach has yielded enormous progress in codifying and predicting those regularities in the universe that are most readily observed. It does not follow, however, as some have come to believe, that unique, one- time events must be excluded from scientific scrutiny, for it is easy to argue that they are occurring all the time and cannot be ignored.
Most events in the world of immediate perception consist of configurations or constellations of both things and processes. That many, if not most, such configurations are complex and unique for all time follows from elementary combinatorics. That is, if one can identify n different things or events in a system, then the number of possible combinations of such objects and events varies roughly as n- factorial (n x [n-1] x [n-2] x … x 3 x 2 x 1.) It doesn’t take a very large n for n! to become immense. Elsasser (1969) called an immense number any magnitude that was comparable to or exceeded the number of simple events that could have occurred since the inception of the universe. To estimate this magnitude, he multiplied the estimated number of protons in the known universe (ca. 1080) by the number of nanoseconds in its duration (ca. 1040.) Whence, any complex system that would take more than 10120 events to be reconstituted by chance from its elements quite simply is not going to reappear. For example, it is often remarked how the second law of thermodynamics is true only in a statistical sense; how, if one waited long enough, a mixture of two types of gas molecules would segregate themselves spontaneously to the respective sides of an imaginary partition. Well, if the number of particles exceeds about 25, the physical reality is that they will never do so.
3 A PROPENSITY FOR HABITS
Elsasser’s conclusion is echoed by Karl Popper (1982), who maintained that the universe is truly open - one where unique contingencies are occurring all the time, everywhere and at all scales. Despite such openness, the world does not become wholly indecipherable, as Peirce’s remark on habits will attest. In order better to apprehend this world of habits, Popper (1990) suggested the need to generalize the Newtonian notion of 'force' into a contingent agency that he called 'propensity'. Looked at the other way around, the forces one sees in nature are only degenerate examples of propensities that happen to be operating in perfect isolation. If such a force connects event, A, with its consequence, B, then every time one observes A, it is followed by B, without exception. Few of the regularities in the complex world that are accessible to the immediate senses behave in this way. What one usually sees is that, if A occurs, most of the time it is followed by B, but not always! Once in a while C results, or D, or E, etc. This is because propensities never occur in isolation from other propensities and are given to interfering with each other to produce unexpected results. Popper did not attempt to quantify his propensities, other than to indicate that they were related in some vague way to conditional probabilities. He advocated the creation of a new 'calculus of conditional probabilities' to treat the dynamics of propensities.
Popper’s call for a new view on what drives events necessarily implies that conventional views on dynamics are inadequate to treat complex systems. The mechanical treatment of events usually deals with two or a small number of elements that are rigidly linked and operate in deterministic fashion. The only situations where very many elements can be considered at one time are those that can be portrayed as wholly stochastic systems, such as the ideal gases of Boltzmann and Gibbs or the equivalent genomic systems of Fisher. In such systems the very many elements either operate independently of each other or interact only very weakly. Furthermore, the massive contingencies that characterize such systems are assumed to exist only at lower scales, and they average out over longer times and larger domains to yield strongly deterministic regularities. By contrast, the orbit of Popper’s 'world of propensities', the excluded middle- ground, encompasses organized habitual behaviors among a moderate number of elements that are loosely, but significantly coupled. The domain of such complex behaviors includes the realm of living systems, and most philosophical attention there has been devoted to ontogenetic development. Ontogeny, however, resembles deterministic behavior perhaps too closely and does not best illustrate the interplay between the organized and the contingent. Hence, the focus in this essay will be upon development as it occurs in ecosystems (Ulanowicz 1986).
In reaction to the argument that unique, one-time events abound in nature, the reader might fell prompted to ask from whence arise the regularities or habits that one sees in the living world? Since Darwin, the conventional answer has been that such order is the result of selection exercised upon the contingent singularities. That is, the welter of singular events is winnowed by what, in evolutionary theory is called (sometimes with almost mystical overtones) 'natural selection'. Now, natural selection is purposefully assumed to operate in independent fashion from outside the system and in a negative fashion in such a way as to eliminate or surpress changes that do not confer advantage to the living configuration - a stance that has been termed 'adaptationism.' The 'advantage' conferred upon the systemis simply, and almost tautologously, that it continues to exist and reproduce, with the result that natural selection imparts no preferred direction to it (Gould 1987.) The arguments for selection in ecosystems contrast radically with the strictures of evolutionary theory. Natural selection is not assumed to be the only agency at work in structuring living systems (Ulanowicz 1997.) In addition, the kinetic structures of the biological processes acting within the systems themselves select (also somewhat tautologously) in favor of those changes that augment their own selection capabilities (see also Taborsky 2002). As a result of such selection the system acquires a distinct orientation that can be quantified, albeit one without a predetermined (teleological) endpoint.
4 HABITS ARISING
To be more explicit, self-selection in ecosystems is thought to arise out of an internal configuration of processes called 'indirect mutualism'. When propensities act in close proximity to one another, any one process will either abet (+), diminish (-) or not affect (0) another. Similarly, the second process can have any of the same effects upon the first. Out of the nine possible combinations for reciprocal interaction, it turns out that one interaction, namely mutualism (+,+), has very different properties from all the rest. The focus here is upon a particular form of such positive feedback called autocatalysis, wherein the effect of each and every link in the feedback loop confers positive effects upon the members it joins.
The action of autocatalysis can be illustrated using the very simple three- component interaction depicted in Figure 1. It is assumed that the action of process A has a propensity to augment a second process B. The emphasis upon the word 'propensity' means that the response of B to A is not wholly obligatory. In keeping with what was written above, A and B are not tightly and mechanically linked. Rather, when process A increases in magnitude, most (but not all) of the time, B also will increase. B tends to accelerate C in similar fashion, and C has the same effect upon A.
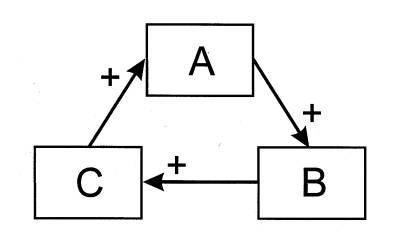
Figure 1: Schematic of a hypothetical 3-component autocatalytic cycle.
A helpful ecological example of autocatalysis is the community that centers around the aquatic macrophyte, Utricularia (Ulanowicz, 1995.) All members of the genus Utricularia are carnivorous plants. Scattered along its feather- like stems and leaves are small bladders, called utricles. Each utricle has a few hair- like triggers at its terminal end, which, when touched by a feeding zooplankter opens the end of the bladder and the animal is sucked into the utricle by a negative osmotic pressure that the plant had maintained inside the bladder. In the field Utricularia plants always support a film of algal growth known as periphyton. This periphyton in turn serves as food for any number of species of small zooplankton. The catalytic cycle is completed when the Utricularia captures and absorbs many of the zooplankton.
Within the framework of the newtonian assumptions autocatalysis usually is viewed merely as a particular type of mechanism. As soon as one admits some form of contingency, however, at least eight other attributes emerge. These behaviors, taken as a whole, comprise a distinctly non-mechanical dynamic. One begins by noting that the very definition of autocatalysis makes it explicitly growth- enhancing. Furthermore, autocatalysis is expressed as a formal structure of kinetic elements. Most germane to the origin of habits, autocatalysis is capable of exerting selection pressure upon its ever-changing constituents. To see this, one supposes that some small change occurs spontaneously in process B. If that change either makes B more sensitive to A or a more effective catalyst of C, then the change will receive enhanced stimulus from A. Conversely, if the change in B either makes it less sensitive to the effects of A or a weaker catalyst of C, then that change will likely receive diminished support from A. Such selection works on the processes or mechanisms as well as on the elements themselves. Hence, any effort to conceive of or simulate development in terms of a fixed set of mechanisms is certain to be inadequate.
It should be noted in particular that any change in B is likely to involve a change in the amounts of material and energy that flow to sustain B. Whence, as a corollary of selection pressure, there arises a tendency to further support those changes that bring ever more resources into B. As this circumstance pertains to all the other members of the feedback loop as well, any autocatalytic cycle becomes the focus of a centripetal vortex, pulling as many resources as possible into its domain (Figure 2.) It is difficult to overemphasize the importance of centripetality in creating a new picture of living systems. It is the property that, more than any other, allows one to distinguish a living agency from its abiotic counterparts. Centripitality constitutes an active agency of a system that does not simply respond to the surroundings. It is causal action directed from the newly- defined entity upon the environment. It is a qualitative break with business as usual.
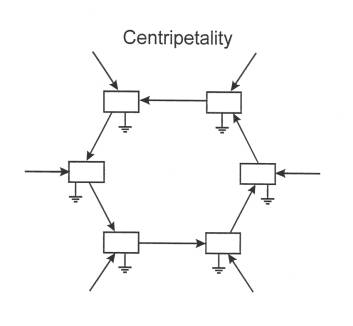
Figure 2: Centripetal flow of resources abetted by autocatalytic selection.
As a consequence of centripetality, whenever two or more autocatalyic loops draw from the same pool of resources, autocatalysis will induce competition. In particular, one notices that whenever two loops partially overlap, the outcome could be the exclusion of one of the loops. In Figure 3, for example, element D is assumed to appear spontaneously in conjunction with A and C. If D is more sensitive to A and/or a better catalyst of C, then there is a likelihood that the ensuing dynamics will so favor D over B, that B will either fade into the background or disappear altogether. That is, selection pressure and the associated centripetality can guide the replacement of elements in a positive way. Of course, if B can be replaced by D, there remains no reason why C cannot be replaced by E or A by F, so that the cycle A,B,C could eventually transform into F,D,E. One concludes that the characteristic lifetime of the autocatalytic form usually exceeds that of most of its constituents. This is not as strange as it may first seem. Despite the fact that (with the exception of neurons) virtually none of the cells that compose human bodies persist more than seven years, and very few of those cells’ constituent atoms remain for more than eighteen months, the identities of individual humans arguably persist for decades.
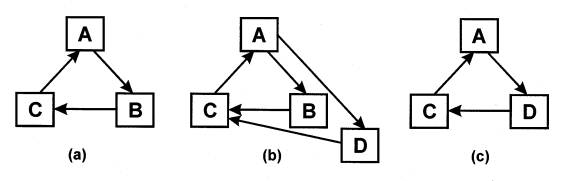
Figure 3: Competition arising from
centripetal action in an autocatalyic loop. (a) Original configuration.
(b) Competition between component B and a new component D, which is either more
sensitive to catalysis
by A or a better catalyst of C. (c) B is replaced by D, and the loop section
A-B-C by that of A-D-C.
Autocatalytic selection pressure and the competition it engenders together define a preferred direction for any developing system - namely, that of ever- more effective autocatalysis. In the terminology of physics this process of establishing certain directions as preferable to others is known as symmetry- breaking. One should not confuse this rudimentary directionality with full- blown teleology, however. It is not necessary, for example, that there exist a pre- ordained endpoint towards which the system strives. The direction of a system at any one instant is defined by its state at the time, and the state changes as the system develops. To distinguish this weaker form of directionality from classical teleology, the Greek word for direction, 'telos' has been employed (Ulanowicz 1997).
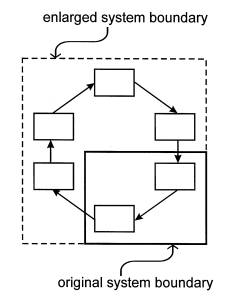
Figure 4: Two hierarchical views of an autocatalytic loop. The original perspective (solid line) includes only part of the loop, which therefore appears to function quite mechanically. A broader vision encompasses the entire loop, and with it the possibility for non-mechanical behaviors.
Taken together, selection pressure, a longer characteristic lifetime and, especially centripetality all constitute evidence for the existence of a degree of autonomy of the larger structure from its constituents. The same characteristics argue against the atomistic idea of breaking the system into components that would continue to function normally (if at all.) In epistemological terms, the dynamics of autocatalysis should be considered emergent behaviors. In Figure 4, for example, if one happens to consider only those elements in the lower right- hand corner (as enclosed by the solid line), then one could identify an initial cause and a final effect. If, however, one expands the scope of observation to include a full autocatalyic cycle of processes (as enclosed by the dotted line), then the system properties just described appear to emerge spontaneously.
Out of the foregoing considerations on autocatalysis one can summarize two major facets concerning its actions: (1) Autocatalysis serves to increase the activities of all its constituents, and (2) it prunes the network of interactions so that those links that most effectively participate in autocatalysis tend to dominante over those that do not. Schematically this transition is depicted in Figure 5. The upper figure represents a hypothetical, inchoate 4- component network before autocatalysis has developed, and the lower one, the same system after autocatalysis has matured. The magnitudes of the flows are represented by the thicknesses of the arrows.
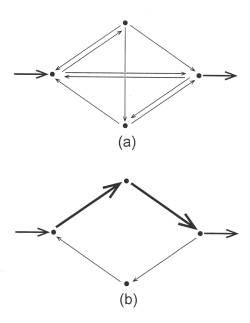
Figure 5: Schematic representation of the major effects that autocatalysis exerts upon a system. (a) Original system configuration with numerous equiponderant interactions. (b) Same system after autocatalysis has pruned some interactions, strengthened others, and increased the overall level of system activity (indicated by the thickening of the arrows.)
As noted, the selection generated by autocatalysis is exerted by the longer- lived configurations upon their smaller, more ephemeral components. Such action is intentionally proscribed by conventional evolutionary theory. As a metaphor for traditional evolution, Daniel Dennett (1995) suggests that the progressive complexity of biological entities resembles 'cranes built upon cranes', whereby new features are hoisted on to the top of a tower of cranes to become the top crane that lifts the next stage into place. He specifically warns against invoking what he calls 'skyhooks', by which he means agencies that create order but have no connection to the firmament.
As a counterpoint to Dennett’s simile, Ulanowicz (2001) has suggested the growth habits of the muscadine grapevine. In the initial stages of growth a lead vine eventually becomes a central trunk that feeds an arboreal complex of grape- bearing vines. In many instances, however, the lateral vines let down adventitious roots to meet the ground some distance from the trunk. In some cases the main trunk actually dies and rots away completely, so that the arboreal pattern of vines comes to be sustained by the new roots, which themselves grow to considerable thickness. No need for skyhooks here! The entity always remains in contact with the firmament, and bottom- up causalities continue to be a necessary part of the narrative. Yet it is the later structures that create connections which eventually replace and displace their earlier counterparts. Top- down causality, the crux of organic behavior, but something totally alien to traditional mechanistic- reductionistic discourse, cannot be ignored. Of course, all similes are imperfect, and one could argue that the muscadine analogy does not lend sufficient attention to historicity, which Dennett’s image seems to overemphasize. But reality is complex, not minimalistic as Dennett maintains, and defies even combinations of simple analogies.
5 QUANTIFYING HABITS
Save for the Utricularia example, references to the precise natures of the various mechanisms that help to channel transfers of material and energy along certain pathways within the ecosystem have not been provided. This, however, is wholly consonant with the semiotic approach to the world. Nonetheless, it has been argued here that the quantification of the partially hidden should also be a legitimate goal of semiotics. Just as probability theory and statistics have been applied to systems of unknown or missing causalities, so also should the actions of hidden constraints be amenable to quantification, even in the absence of their explicit descriptions. Because ecosystems appear to be a rich resevoir of semiotic behaviors, the reader’s attention is now directed towards networks of trophic interactions among ecological constituents.
Quantification often is facilitated by focussing upon
some palpable, conservative medium of structure and exchange. Accordingly, the
transfer of material or energy from prey (or donor) i to predator (or receptor)
j will be denoted as Tij, where i and j range over all members of a
system with n elements. The total amounts flowing into or out of any
compartment i then become T.i = Sj
Tji and Ti. = Sj
Tij, respectively, where the dot in place of a subscript indicates
summation over that index. The total activity of the system can then be
measured as the simple sum of all system processes, ![]() ,
or what has been called the “total system throughput”. Growth, the first major
outcome of autocatalysis, thereby will be represented by an increase in the
total system throughput, much as economic growth is reckoned by any increase in
Gross Domestic Product. The transfers, Tij, for the major taxa
comprising the ecosystem of the Chesapeake Bay are depicted in Figure 6.
,
or what has been called the “total system throughput”. Growth, the first major
outcome of autocatalysis, thereby will be represented by an increase in the
total system throughput, much as economic growth is reckoned by any increase in
Gross Domestic Product. The transfers, Tij, for the major taxa
comprising the ecosystem of the Chesapeake Bay are depicted in Figure 6.
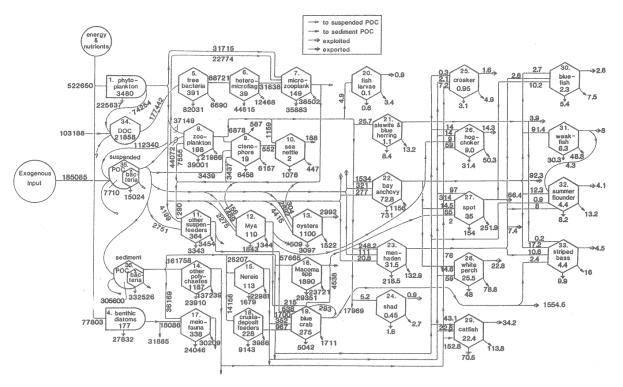
Figure 6:
Estimated exchanges of carbon among the 36 main components of the mesohaline
Chesapeake Bay
ecosystem (Baird and Ulanowicz 1989.) “Bullets” represent primary producers
(flora); hexagons, fauna; and
‘birdhouses’, nonliving storage pools. Flows measured in mgC/m2/y,
stocks (numbers inside the boxes) in mgC/m2.
The second, more interesting action of the hidden (autocatalytic) system constraints is that they channel progressively more material along certain pathways at the relative expense of flows among other members. As prelude to quantifying such selection one notes that, if hidden constraints are channeling flow from some component, i, to some other species, j, then the frequency of flow along this link should be greater than what would be calculated according to pure chance. Now, the observed frequency with which medium is channeled from i to j by such constraints can be estimated by the quotient (Tij/T..). The frequency with which flow leaves compartment i is estimated by (Ti./T..) and that with which it enters j by (T.j/T..), so that the frequency with which medium would make its way from i to j by pure chance would be given by the joint probability, (Ti.T.j/T2..). Because constraints work to augment flow from i to j, the former probability should be greater than chance, i.e., (Tij/T.. > Ti.T.j/T2..).
In order to quantify the degree by which channeled flow exceeds pure chance, it is useful to define the 'potential for constraint' as the logarithm of the probability of a given flow. That is, the potential for constraint associated with the observed flow from i to j becomes log(Tij/T..). Similarly, the potential for constraint of flow from i reaching j via arbitrary random pathways would be log(Ti.T.j/T2..). The difference between these potentials becomes the propensity for flow from i to j, Pij. That is, a measure for propensity is the amount by which the potential under constraint exceeds the potential under pure chance. Algebraically, Pij = log(Tij/T..) - log(Ti.T.j/T2..), or, after combining the logarithms, simply log(TijT../Ti.T.j).
According to conventional probability theory, the expected value of any distributed quantity is a close approximation to its average and can be estimated by multiplying the magnitude of each category in the distribution by the probability that an element belongs to that category, and then summing over all such products. Because the estimated probability of flow from i to j is Tij/T.., the average propensity, or average mutualconstraint (AMC) thereby becomes:
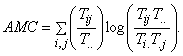
To demonstrate how an increase in AMC actually tracks the autocatalyic 'pruning' process, the reader is referred to the three hypothetical configurations in Figure 7. In configuration (a) the distribution of medium leaving any one compartment is maximally indeterminate, and AMC is identically zero. The possibilities in network (b) are somewhat more constrained. Flow exiting any compartment can proceed to only two other compartments, and the AMC rises accordingly. Finally, flow in schema (c) is maximally constrained, and the AMC assumes its maximal value for a network of dimension 4.
Because autocatalysis is a unitary process that affects both the magnitudes of exchanges and the flow structure, it is possible to incorporate both factors of growth and development into a single index by multiplying them together to yield a measure called the system ascendency, A = T.. x AMC, or
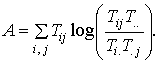
In his seminal paper, 'The strategy of ecosystem development', Eugene Odum (1969) identified 24 attributes that characterize more mature ecosystems. These can be grouped into categories labeled species richness, dietary specificity, recycling and containment. All other things being equal, a rise in any of these four attributes also serves to augment the ascendency. Odum’s phenomenological observations can thereby be reinterpreted as showing that “in the absence of major perturbations, ecosystems have a propensity to increase in ascendency.” Increasing ascendency is a quantitative way of expressing the tendency for those system elements that are in catalytic communication to reinforce each other at the relative expense of non- participating members. It traces the ascent of habits within a system.
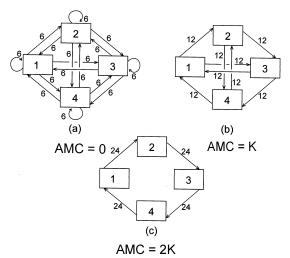
Figure 7: (a) The most equivocal distribution of 96 units of transfer among
four system components.
(b) A more constrained distribution of the same total flow. (c) The maximally
constrained pattern of 96 units of transfer involving all four components. AMC
= ‘average mutual constraint.’
6 FREEDOM FROM HABITS
It must be emphasized in the strongest terms possible that increasing ascendency is only half the story. Ascendency accounts for how efficiently and coherently the system processes medium - for how closely habits approach the status of mechanism. Using the same type of mathematics (Ulanowicz and Norden, 1990), however, one can compute as well a complementary index called the system overhead, F, such that:
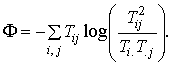
In contrast to ascendency, overhead quantifies the degrees of freedom, inefficiencies and incoherencies that remain in a system. Although these latter properties usually encumber overall system performance at processing medium, they become absolutely essential to system survival whenever the system incurs a novel perturbation. At such time, the overhead becomes the repertoire from which the system can draw to adapt to the new circumstances. Without sufficient overhead, a system is unable create an effective response to the exigencies of its environment.
The reader may readily verify that the sum, C = A + F, represents the variety of processes extant in the system as scaled by the total system activity (T..). The sum C is referred to elsewhere as the system capacity (Ulanowicz and Norden 1990.) That A and C are complementary indicates a fundamental tension between the two attributes. When environmental conditions are not too rigorous (as one might find in a tropical rain forest, for example), then a tendency for A to increase at the expense of F will occur. The configurations observed in nature appear, therefore, to be the results of two antagonistic tendencies (ascendency vs. overhead), which interact in the manner of a Hegelian dialectic: Whereas the tendency for A to rise describes the process of development, it is constantly being countered by the opposite (but necessary) tendency towards disorder and incoherence. Yet sufficient amounts of both attributes are necessary for the system to persist over the long term.
Referring again to Figure 6, one notes that, no matter how complex the network of trophic exchanges might be, it is a straightforward (albeit sometimes tedious) process to calculate the system ascendency and overhead. That is, between a system’s ascendency and its overhead one has a sure way of partitioning the complexity of a system into a fraction that, respectively, characterizes organized behavior and a complement thereof that represents the degrees of freedom remaining in the system for reconfiguration. One may also quantitatively track changes in these two partitions over time; i.e., one can follow the ecological dynamic as it unfolds.
7 THE ECOLOGICAL DYNAMIC
With the foregoing as background, it is now possible to outline the basic operation of the ecological dynamic: Original events may arise at any scale. Most vanish, however, without leaving a trace. Some simply accumulate as neutral elements. Occasionally, deleterious configurations appear, but these are damped by the internal selection process. On rare occasions a novel event occurs that resonates with the existing autocatalyic configurations and is embodied into (selected for) the evolving kinetic structure. The effect of any one event does not propagate universally; it is always constrained by selection processes at other levels. Ascendency tends to grow at the expense of overhead, but systems can go too far in this direction. Some overhead is always necessary as a reservoir from which the system can create new stabilizing responses to novel perturbations.
It should be growing apparent that the elements of the ecological dynamic do not accord well with the conventional assumptions that were enumerated in the Newtonian worldview. In fact, there seem to exist conflicts concerning each and every assumption. Accordingly, it becomes necessary to formulate a new set of tentative assumptions that accord better with how ecosystems appear to be developing:
(1’) Ecosystems are not causally closed. They appear to be open to the influence of non- mechanical agency. Spontaneous events may occur at any level of the hierarchy at any time. Mechanical causes usually originate at scales inferior to that of observation, and their effects propagate upwards. Larger- scale agencies and constraints appear at the focal level and higher levels and their influences propagate downwards (Salthe, 1985; Ulanowicz, 1997.)
(2’) Ecosystems are not deterministic machines. They are contingent in nature. Biotic actions resemble propensities more than mechanical forces.
(3’) The realm of ecology is granular, rather than universal. Models of agencies and constraints at any one scale can explain matters at another scale only in inverse proportion to the remoteness between them. Conversely, the domain within which irregularities and perturbations can damage a system is usually circumscribed. Chance does not necessarily unravel a system.
(4’) Ecosystems, like other biotic systems, are not reversible, but instead historical. Contingencies often take the form of discontinuities, which degrade predictability into the future and obscure hindcasting. The effects of past discontinuities are often retained (as memories) in the material and kinetic forms that result from adaptation. Time takes a preferred direction or telos in ecosystems - that of increasing ascendency.
(5’) Ecosystems are not easily decomposed; they are organic in composition and behavior. Propensities never exist in isolation from other propensities, and communication between them fosters clusters of mutually reinforcing propensities to grow successively more interdependent. Hence, the observation of any component in isolation (if possible) reveals regressively less about how it behaves within the ensemble.
Ulanowicz (1999) has called this set of alternative assumptions an ecological metaphysic. It must be acknowledged, however, that it represents but one possible alternative to conventional science. Although some might regard the suggested metaphysic as a deconstructivist threat to science, others hopefully will see is as a necessary relaxation of strictures that may have been inhibiting more fruitful approaches to understanding natural living systems. It was in this vein that Bauman (1992, Cillers 1998) wrote that 'Modernity was a long march to prison.', and excessive rigidity should not be confused with rigor in science.
In no way should the reader consider the mathematics proffered here as analogous to the bars that seal off Bauman’s prison. Despite the coincident rise of mathematics with that of modern science, one should not disqualify quantitative methods out of hand. They have the potential to play an integral and useful part in the postmodern, semiotic description of nature. That something remains hidden from view does not foreclose the possibility that its effects can be adequately gauged and tracked. Although much of ecosystem dynamics must necessarily remain semiotic and tacit, it appears that much of what lies below the surface can be described using Popper’s recommended conditional probabilities. It may yet prove that ascendency theory will provide one of the early elements to an evolving quantitative semiotics that will yield significant benefits for postmodern science.
8 ACKNOWLEDGEMENTS
The author was supported in part by the National Science Foundation’s Program on Biocomplexity (Contract No. DEB-9981328.) and the US Geological Survey Program for Across Trophic Levels Systems Simulation (ATLSS, Contract 1445CA09950093).
REFERENCES
Baird, D. and R.E. Ulanowicz. 1989. The seasonal dynamics of the Chesapeake Bay ecosystem. Ecol. Monogr. 59:329 -364.
Bauman, Z. 1992. Intimations of Postmodernity. Routledge: London. p. xvii.
Cillers, P. 1998. Complexity and Postmodernism: Understanding complex systems. Routledge: London. p. 138.
Dennett, D.C 1995. Darwin’s Dangerous Idea: Evolution and the Meanings of Life. Simon and Schuster: New York.
Depew, D.J. and B.H. Weber. 1994. Darwinism Evolving: Systems Dynamics and the Geneology of Natural Selection. MIT Press: Cambridge, MA.
Elsasser, W.M. 1969. Acausal phenomena in physics and biology: A case for reconstruction. American Scientist 57(4):502-516.
Gould, S.J. 1987. Time's Arrow, Time's Cycle : Myth and Metaphor in the Discovery of Geological Time. Harvard University Press: Cambridge, Massachusetts.
Hoffmeyer, J. 1993. Signs of Meaning in the Universe. Indiana University Press: Bloomington, Indiana.
Odum, E.P. 1969. The strategy of ecosystem development. Science. 164:262-270.
Popper, K.R. 1982. The Open Universe: An Argument for Indeterminism. Rowman and Littlefield: Princeton, New Jersey.
Popper, K.R. 1990. A World of Propensities. Thoemmes: Bristol.
Salthe, S.N. 1985. Evolving Hierarchical Systems: Their Structure and Representation. Columbia University Press: New York.
Taborsky, E. 2002. Energy and Evolutionary Semiosis. Sign System Studies 30(1): 361-381.
Ulanowicz, R.E. 2001. The organic in ecology. Ludus Vitalis 9(15):183-204.
--------- 1997. Ecology, the Ascendent Perspective. Columbia University Press: New York.
-------- 1995. Utricularia's secret: The advantages of positive feedback in oligotrophic environments. Ecological Modelling 79:49-57.
------- 1986. Growth and Development: Ecosystems Phenomenology. Springer- Verlag: New York. (Reprinted 2000 by toExcel Press: San Jose, CA.)
Ulanowicz, R.E., and J.S. Norden. 1990. Symmetrical overhead in flow networks. International Journal of Systems Science 1:429-437.