Physical Theory of
Information Processing in the Mind: Concepts and Emotions
©This paper is not for reproduction without the express permission of the author.
ABSTRACT
The paper discusses a possibility that a multiplicity of mind phenomena can be understood from few fundamental principles of the mind organization, which are mathematically formulated. The paper discusses the role of concepts and emotions in the information processing by the mind and identifies an “elementary thought process” in which an event (in the outside world, or inside the mind) is understood as a concept. Previous attempts in artificial intelligence at describing thought processes are briefly reviewed and their fundamental (mathematical) limitations are discussed. The role of emotional signals in overcoming these past limitations is emphasized. An elementary thought process is related to semiotical notions of signs and symbols. It is further related to understanding, imagination, intuition, and to the role of aesthetic emotions and beauty in functioning of the mind. Relationships between the mind and brain are briefly discussed. All the discussed notions are grounded in psychological data and mathematical theory, yet knowledge of mathematics is not assumed, discussions related to the mathematical theory are given conceptually, and the paper is accessible to non-mathematicians. A theory described here could possibly serve as a prolegomenon to a physical theory of mind.
keywords: mind, physics, semiotics, symbols, fuzzy dynamic logic, neural networks, emotions, concepts, intelligent systems, aesthetics, beauty.
1 physics and mathematics of mind
After creating a physical theory of the material world Newton devoted his life to developing a science of the mind, the physics of spiritual substance (Westfall 1983). Newton failed at his second project and many contemporary physicists are still afraid to look at mind as a physical system. This paper is an attempt to overcome this timidity and to demonstrate that many of the mind phenomena can be explained from a few basic principles that can be mathematically formulated, which is the essence of the physical theory. Words like mind, thought, imagination, emotion, concept, aesthetics, beauty are not often encountered alongside physics or mathematics. People use these words in many ways colloquially, but their use in science and especially in mathematics of intelligence has not been uniquely defined and is a subject of active research and ongoing debates [1]. According to a dictionary (AHCD), mind includes conscious and unconscious processes, especially thought, perception, emotion, will, memory, and imagination, and it originates in brain. These constituent notions will be discussed throughout the paper.
A broad range of opinions exists on the mathematical methods suitable for the description of the mind. Founders of artificial intelligence thought that formal logic was sufficient (Newell 1983) and no specific mathematical techniques would be needed to describe the mind (Minsky 1988). An opposite point of view is that there are few specific mathematical constructs, “the first principles” of mind. Among researchers taking this view is Grossberg, who suggested that the first principles include a resonant matching between lower-level signals (Grossberg 1988) and higher-level representations and emotional evaluation of conceptual contents (Grossberg and Levine 1987); Josephson, Meystel, Zadeh, and the author suggested specific principles of the mind organization (Josephson 1997; Meystel 1995; Zadeh 1997; Perlovsky 2001) [2] . Hameroff, Penrose, and the author (among others) considered quantum computational processes that might take place in the brain (Hameroff 1994; Penrose 1994; Perlovsky 2001). Although, it was suggested that new unknown yet physical phenomena will have to be accounted for explaining the working of the mind (Josephson 1997; Penrose 1994). This paper describes mechanisms of mind that can be “implemented” by classical-physics mechanisms of the brain neural networks.
2 theories of mind and combinatorial complexity
Understanding signals coming from sensory organs involves associating subsets of signals corresponding to particular objects with internal representations of these objects. This leads to recognition of the objects and activates internal brain signals leading to mental and behavioral responses that constitute the understanding of the meaning (of the objects).
Developing mathematical descriptions of the very first recognition step of this seemingly simple association-recognition-understanding process has not been easy, a number of difficulties have been encountered during the past fifty years. These difficulties have been summarized under the term combinatorial complexity (CC) (Perlovsky 2001). The problem was first identified in pattern recognition and classification problems in the 1960s and was named “the curse of dimensionality” (Bellman 1961). The following thirty years of developing adaptive statistical pattern recognition and neural network algorithms designed for self-learning led to a conclusion that these approaches often encountered CC of learning requirements: recognition of any object, it seemed, could be learned if “enough” training examples could be used for an algorithm self-learning. The required examples had to account for all possible variations of “an object”, in all possible geometric positions, in all combinations with other objects, sources of light, etc., leading to astronomical numbers of required examples. By the end of the 1960s a different paradigm became popular: rule-based systems (or expert systems) were proposed to solve the problem of learning complexity. An initial idea was that rules would capture the required knowledge and eliminate a need for learning. Rule systems work well when all aspects of the problem can be predetermined. However, rule systems and expert systems in the presence of unexpected variability, encountered CC of rules: more and more detailed sub-rules and sub-sub-rules had to be specified. In 1980s model-based systems became popular, which were proposed to combine advantages of adaptivity and rules by utilizing adaptive models, but they encountered computational CC (N and NP complete algorithms). The CC became a ubiquitous feature of intelligent algorithms and seemingly, a fundamental mathematical limitation. The reason was that considered algorithms had to evaluate multiple combinations of elements and the number of combinations is very large: say, take 100 elements (not too large a number), but the number of combinations of 100 elements is 100100, a number larger than the number of elementary particles in a Universe, and no computer would ever be able to compute that many combinations.
Combinatorial complexity has been related to the type of logic, underlying various algorithms and neural networks (Perlovsky 1998a). Formal logic is based on the “law of excluded third”, according to which every statement is either true or false and nothing in between. Therefore, algorithms based on formal logic have to evaluate every little variation in data or internal representations as a separate logical statement; a large number of combinations of these variations causes combinatorial complexity. In fact, combinatorial complexity of algorithms based on logic has been related to the Gödel theory: it is a manifestation of the incompleteness of logic in finite systems (Perlovsky 1996a). Multivalued logic and fuzzy logic were proposed to overcome limitations related to the law of excluded third (Jang et al 1996). Yet the mathematics of multivalued logic is no different in principle from formal logic. Fuzzy logic encountered a difficulty related to the degree of fuzziness: if too much fuzziness is specified, the solution does not achieve a needed accuracy, if too little, it might become similar to formal logic.
The seemingly fundamental nature of the mathematical difficulties discussed above led many to believe that classical physics cannot explain the working of the mind. Yet, I would like to emphasize another aspect of the problem: often mathematical theories of the mind were proposed before the necessary physical intuition of how the mind works was developed. Newton, as often mentioned, did not consider himself as evaluating various hypothesis about the working of the material world, he felt that he possessed an intuition (Westfall 1983), or what we call today a physical intuition about the world. A particular intuition about the mind is that it operates with emotions. An essential role of emotions in the working of the mind was analyzed from the psychological and neural perspective by Grossberg (1987) from the neuro-physiological perspective by Damasio (1995) and from the learning and control perspective by the author (Perlovsky 1998b, 1999). One reason for the engineering community being slow in adopting these results is the cultural bias against emotions as a part of thinking processes. Plato and Aristotle thought that emotions are “bad” for intelligence, this is a part of our cultural heritage, and the founders of Artificial Intelligence repeated it. Yet, as discussed in the next section, combining conceptual understanding with emotional evaluations might be crucial for overcoming the combinatorial complexity as well as the related difficulties of logic.
Let me summarize briefly and in the most simplified way several aspects of the working of the mind as it is understood today, which might be crucial to the development of the theory of the mind. Mind emerged in evolution for the purpose of survival and therefore it serves for a better satisfaction of the basic instincts, which emerged as survival mechanisms even before mind. Instincts operate like internal sensors: for example, when the sugar level in the blood goes below a certain level an instinct “tells us” to eat. That which is most accessible to our consciousness mechanism of the mind, are concepts: the mind operates with concepts. Concepts are like internal models of the objects and situations.
What is the relationship between instincts and concepts and what is the mechanism relating them? An ability for concepts evolved for instinct satisfaction and emotions are neuronal signals connecting instinctual and conceptual brain regions. Whereas in colloquial usage, emotions are often related to facial expressions, higher voice pitch, exaggerated gesticulation — these are the outward signs of emotions, serving for communication. A more fundamental role of emotions within the mind system is that emotional signals evaluate concepts for the purpose of instinct satisfaction. This evaluation is not according to rules or concepts (as in rule-systems of artificial intelligence), but according to a different instinctual-emotional mechanism described in the next section. This emotional mechanism is crucial for breaking out of the “vicious circle” of combinatorial complexity.
The result of conceptual-emotional understanding of the world are actions (or behavior) in the outside world or within the mind. In this paper we touch on only one type of behavior, the behavior of improving understanding and knowledge about the world (and self). In the next section we describe in notional terms with a minimum of mathematics, a mathematical theory of a “simple” conceptual-emotional recognition and understanding. As we will discuss, in addition to concepts and emotions, it involves with necessity mechanisms of intuition, imagination, conscious, unconscious, and aesthetic emotion. And this process is intimately connected to an ability of mind to form symbols and interpret signs.
Mind involves a hierarchy of multiple levels of concept-models, from simple perceptual elements (like an edge, or a moving dot), to concept-models of object, to complex scenes, and up the hierarchy toward the concept-models of the meaning of life and purpose of our existence. Hence the tremendous complexity of the mind, yet relatively few basic principles of the mind organization go a long way explaining this system.
Modeling field theory (Perlovsky 2001), (summarized below, associates lower-level signals with higher-level concept-models (or internal representations), resulting in an understanding of signals, while overcoming the difficulties of CC described in Section 2. It is achieved by using measures of similarity between the concept-models and the input signals combined with a new type of logic, the fuzzy dynamic logic. Modeling field theory is a multi-level, hetero-hierarchical system. This section describes a basic mechanism of interaction between two adjacent hierarchical levels of signals (fields of neural activation); sometimes, it will be more convenient to talk about these two signal-levels as an input to and output from a (single) processing-level.
At each level, the output are concepts recognized (or formed) in input signals. Input signals X are associated with (or recognized, or grouped into) concepts according to the representations-models and similarity measures at this level. In the process of association-recognition, models are adapted for better representation of the input signals; and similarity measures are adapted so that their fuzziness is matched to the model uncertainty. The initial uncertainty of models is high and so is the fuzziness of the similarity measure; in the process of learning models become more accurate and the similarity measure more crisp, the value of the similarity increases. I call this mechanism fuzzy dynamic logic. Let me repeat again: knowledge of mathematics is not required to read the following, the mathematical equations given below could be just skipped, their meanings are explained in plain language.
4.1 Internal Models, Learning, and Similarity
During the learning process, new associations of input signals are formed resulting in the evolution of new concepts. Input signals {X(n)}, is a field of input neuronal synapse activation levels, n enumerates the input neurons and X(n) are the activation levels; a set of concept-models {h} is characterized by the models (representations) {Mh(n)} of the signals X(n); each model depends on its parameters {Sh}. In a highly simplified description of a visual cortex, n enumerates the visual cortex neurons, X(n) are the “bottom-up” activation levels of these neurons coming from the retina through visual nerve, and Mh(n) are the “top-down” activation levels (or priming) of the visual cortex neurons from previously learned object-models[3]. The learning process attempts to “match” these top-down and bottom-up activations by selecting “best” models and their parameters. Mathematically, learning increases a similarity measure between the sets of models and signals, L({X(n)},{Mh(n)}). The similarity measure is a function of model parameters and associations between the input synapses and concepts-models. It is constructed in such a way that any of a large number of objects can be recognized, no matter if they appear on the left or on the right. Correspondingly, a similarity measure is designed so that it treats each concept-model as an alternative for each subset of signals
L({X},{M}) = ![]() r(h) l(X(n) | Mh(n));
(1)
r(h) l(X(n) | Mh(n));
(1)
here l(X(n)|Mh(n)) (or simply l(n|h)) is a conditional partial similarity between one signal X(n) and one model Mh(n), and all possible combinations of signals and models are accounted for in this expression. Parameters r(h) are proportional to the number of signals {n} associated with the model h.
In the process of learning, concept-models are constantly modified. From time to time a system forms a new concept, while retaining an old one as well; alternatively, old concepts are sometimes merged. [Formation of new concepts and merging of old ones require a modification of the similarity measure (1); the reason is that more models always result in a better fit between the models and data. This is a well known problem, it can be addressed by reducing (1) using a “penalty function”, p(N,M) that grows with the number of models M, and this growth is steeper for a smaller amount of data N. For example, an asymptotically unbiased maximum likelihood estimation leads to multiplicative p(N,M) = exp(-Npar/2), where Npar is a total number of adaptive parameters in all models (this penalty function is known as Akaike Information Criterion, see (Perlovsky 2001) for further discussion and references)].
4.2 Fuzzy dynamic logic and MFT
The learning process consists in estimating model parameters Sh and associating subsets of signals with concepts by maximizing the similarity (1). Note, that (1) contains a large number of combinations of models and signals, a total of HN items; this was a cause for the combinatorial complexity of the past algorithms discussed previously.
Modeling field theory (MFT) solves this problem by utilizing fuzzy dynamic logic (Perlovsky 2001; Perlovsky 1996b, 1997). MFT introduces association variables f(h|n)
f(h|n)
= r(h) l(n|h) /![]() r(h') l(n|h'). (2)
r(h') l(n|h'). (2)
These variables give a measure of correspondence between a signal X(n) and a model Mh relative to all other models, h’. A mechanism, an internal dynamics, of the Modeling Fields (MF) is defined as follows,
df(h|n)/dt
= f(h|n)![]() {[dhh' -
f(h'|n)]·[∂lnl(n|h')/∂Mh'] ¶M'h'/¶Sh'·dSh'/dt, (3)
{[dhh' -
f(h'|n)]·[∂lnl(n|h')/∂Mh'] ¶M'h'/¶Sh'·dSh'/dt, (3)
dSh/dt={∫Nf(h|n)[∂lnl(n|h)/∂Mh]¶M'h/¶Sh, (4)
here dhh' is 1 if h=h', 0 otherwise. Parameter t is the time of the internal dynamics of the MF system (like a number of internal iterations). The following theorem was proven.
Theorem. Equations (2) through (4) define a convergent dynamic system MF with stationary states defined by max{Sh}L.
In plain language this means that the above equations indeed result in concept-models in the “mind” of the MFT system, which are most similar [in terms of similarity (1)] to the sensory data. Despite a combinatorially large number of items in (1), a computational complexity of the MF method is relatively low, it is linear in N, it could be implemented by a physical system (like the brain) and therefore it may correspond to the working of the mind. These equations describe a closed loop system, which is illustrated in the block-diagram in Fig. 1. A reference to the closed loop emphasizes that the loop can sustain its operations on its own, the loop is not entirely closed in that there are input data into the loop and output concepts from the loop.
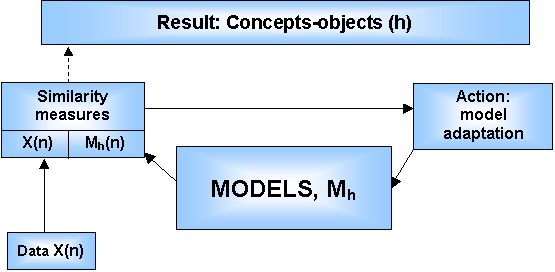
Figure 1: For a single level of MFT, input signals are unstructured data {X(n)} and output signals are recognized or formed concepts {h}. The MFT equations (2) through (4) describe a continuous closed-loop operation involving input data, similarity measures, models, and actions of the model adaptation.
4.3 MFT hierarchical organization
The previous sub-section described a single processing layer in a hierarchical MFT system. An input to each layer is a set of signals X(n), or in neural terminology, an input field of neuronal activations. An output are the activated models Mh(Sh,n); it is a set of models or concepts recognized in the input signals. Equations (2-4) describe a loop-process: at each iteration (or internal-time t) the l.h.s. of the equations contain association variables f(h|n) and other model parameters computed at the previous iteration. In other words, the output models “act” upon the input to produce a “refined” output models (at the next iteration). This process is directed at increasing the similarity between the models and signals. It can be described as an internal behavior generated by the models.
The output models initiate other actions as well. First, activated models (neuronal axons) serve as input signals to the next processing layer, where more general concept-models are recognized or created. Second, concept-models along with the corresponding instinctual signals and emotions may activate behavioral models and generate behavior directed into the outside world (a process not contained within the above equations). In general, a higher level in a hierarchical system provides a feedback input into a lower level. For example, sensitivity of retinal ganglion cells depends on the objects and situations recognized higher up in the visual cortex; or a gaze is directed based on which objects are recognized in the field of view. More complete interactions within this hierarchical organization are illustrated in Fig.2.
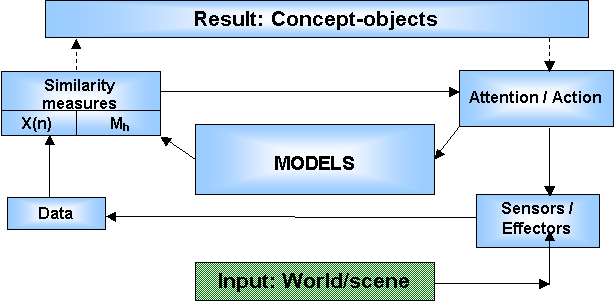
Figure 2: More details of integrated interactions are shown for a single-level loop of MFT at the bottom of the hierarchy: input data X(n) are coming from the outside world through sensors; sensors and effectors are acting in the surrounding world based on the results of information processing inside the MFT system.
Concept-objects identified at the output of the lower level of MFT system in Fig.2 become input signals to the next MFT level which identifies more general concepts of relationships among objects and situations; at the same time more general concepts of understanding identified at a higher level activate behavioral concept-models that affect processes at a lower level. The agent processes, or the loop-processes of model-concept adaptation, understanding and behavior generation continue up and down the hierarchy of the MFT levels.
The loop of operations of MFT can be better described as multiple loops each involving a model; to some extent these multiple loops are independent, yet some models interact when they are associated with the same data pieces. Therefore MFT is an intelligent system composed of multiple adaptive intelligent agents which possess a degree of autonomy yet interact among themselves. Each concept-model along with the similarity measure and behavioral response is a continuous loop of operations, interacting with other agents from time to time; an agent is "dormant" until activated by a high similarity value. When activated, it is adapted to the signals and other agents, so that the similarity increases. Every piece of signal may activate several concepts, or agents, in this way data provide evidence for the presence of various objects (or concepts). Agents compete with each other for evidence (data), while adapting to the new signals.
Equations (2-4) describe an elementary process of perception or cognition, in which a large number of model-concepts compete for incoming signals, model-concepts are modified and new ones are formed, and eventually, more or less definite connections [high or low values of f(h|n), varying between 0 and 1] are established among signal subsets on the one hand, and model-concepts on the other. Perception refers to processes in which the input signals come from sensory organs and model-concepts correspond to objects in the surrounding world. Cognition refers to higher levels in the hierarchy where the input signals are concepts activated at lower levels and model-concepts are more complex and correspond to situations and relationships among lower-level concepts.
A salient mathematical property of this processes ensuring a smooth convergence is a correspondence between uncertainty in models (that is, in the knowledge of model parameters) and uncertainty in associations f(h|n). In perception, as long as model parameters do not correspond to actual objects, there is no match between models and signals; many models poorly match many objects, and associations remain fuzzy (nor 1 nor 0). Eventually, one model (h') wins a competition for a subset {n'} of input signals X(n), when parameter values match object properties, and f(h'|n) values become close to 1 for nÎ{n'} and 0 for nÏ{n'}. This means that this subset of data is recognized as a specific object (concept). Upon the convergence, the entire set of input signals {n} is divided into subsets, each associated with one model-object, uncertainties become small, and fuzzy a priori concepts become crisp concepts. Cognition is different from perception in that models are more general, more abstract, and input signals are the activation signals from concepts identified (cognized) at a lower hierarchical level; the general mathematical laws of cognition and perception are similar in MFT and constitute a basic principle of the mind organization. Let us discuss relationships between the MFT theory and concepts of mind developed in psychology, philosophy, linguistics, aesthetics, neuro-physiology, neural networks, artificial intelligence, pattern recognition, and intelligent systems.
5.2 Elementary thought-process, conscious and unconscious
A thought-process or thinking involves a number of sub-processes and attributes, including internal representations and their manipulation, attention, memory, concept formation, knowledge, generalization, recognition, understanding, meaning, prediction, imagination, intuition, emotion, decisions, reasoning, goals, behavior, conscious and unconscious (Grossberg 1988; Meystel 1995; Perlovsky 2001).
A “minimal” subset of these processes has to involve mechanisms for afferent and efferent signals, (Grossberg, 1988), in other words, bottom-up and top-down signals coming from outside (external sensor signals) and from inside (internal representation signals). According to Carpenter and Grossberg (1987) every recognition and concept formation process involves a “resonance” between these two types of signals. In MFT, at every level in a hierarchy the afferent signals are represented by the input signal field X, and the efferent signals are represented by the modeling field signals Mh; resonances correspond to high similarity measures l(n|h) for some subsets of {n} that are “recognized” as concepts (or objects) h. The mechanism leading to the resonances is given by (2-4), and we call it an elementary thought-process. The elementary thought-process involves elements of conscious and unconscious processes, imagination, memory, internal representations, concepts, instincts, emotions, understanding and behavior as further described later.
A description of working of the mind as given by the MFT dynamics was first provided by Aristotle, describing thinking as a learning process in which an a priori form-as-potentiality (fuzzy model) meets matter (sensory signals) and becomes a form-as-actuality (a concept). Jung suggested that conscious concepts are developed by mind based on genetically inherited structures of mind, archetypes, which are inaccessible to consciousness (1934) and Grossberg (1988) suggested that only signals and models attaining a resonant state (that is signals matching models) reach consciousness.
In the elementary thought process, subsets in the incoming signals are associated with recognized model-objects, creating phenomena (of the MFT-mind) which are understood as objects, in other words signal subsets acquire meaning (e.g., a subset of retinal signals acquires a meaning of a chair). There are several aspects to understanding and meaning. First, object-models are connected (by emotional signals: Grossberg and Levine 1987, Perlovsky 2001; Perlovsky 1998b) to instincts that they might satisfy, and also to behavioral models that can make use of them for instinct satisfaction. Second, an object is understood in the context of a more general situation in the next layer consisting of more general concept-models, which accepts as input-signals the results of object recognition. That is, each recognized object-model (phenomenon) sends (in neural terminology, activates) an output signal; and a set of these signals comprises input signals for the next layer models, which ‘cognize’ more general concept-models. And this process continues up and up the hierarchy of models and mind toward the most general models a system could come up with, such as models of universe (scientific theories), models of self (psychological concepts), models of the meaning of existence (philosophical concepts), models of a priori transcendent intelligent subjects (theological concepts).
Imagination involves excitation of a neural pattern in a visual cortex in the absence of an actual sensory stimulation (say, with closed eyes) (Grossberg 1988). Imagination was often considered to be a part of thinking processes; Kant (1790) emphasized the role of imagination in the thought process, he called thinking “a play of cognitive functions of imagination and understanding”. Whereas the pattern recognition and artificial intelligence algorithms of the recent past would not know how to relate to this (Newell 1983; Minsky 1988), the Carpenter and Grossberg resonance model (1987) and the MFT dynamics both describe imagination as an inseparable part of thinking: imagined patterns are top-down signals that prime the percepting cortex areas (priming is a neural terminology for making neural cells to be more readily excited). In MFT, the imagined neural patterns are given by models Mh. MFT (in agreement with neural data) just adds details to Kantian description: thinking is a play of higher-hierarchical-level imagination and lower-level understanding. Kant identified this “play” [described by (3-6) or (7-12)] as a source of aesthetic emotion; modeling aesthetic emotion in MFT is described later.
Historically, the mind is described in psychological and philosophical terms, whereas the brain is described in terms of neurobiology and medicine. Within scientific exploration the mind and brain are different description levels of the same system. Establishing relationships between these description is of great scientific interest. Today we approach solutions to this challenge (Grossberg 2000), which eluded Newton in his attempt to establish physics of “spiritual substance”(Westfall 1983). General neural mechanisms of the elementary thought process (which are similar in MFT and ART (Carpenter and Grossberg, 1987) have been confirmed by neural and psychological experiments, this includes neural mechanisms for bottom-up (sensory) signals, top-down “imagination” model-signals, and the resonant matching between the two (Grossberg 1988; Zeki 1993; Freeman 1975). Adaptive modeling abilities are well studied with adaptive parameters identified with synaptic connections (Koch and Segev 1998; Hebb 1949); instinctual learning mechanisms have been studied in psychology and linguistics (Piaget 2000; Chomsky 1981; Jackendoff 2002; Deacon 1998).
Functioning of the mind and brain cannot be understood in isolation from the system’s “bodily needs”. For example, a biological system (and any autonomous system) needs to replenish its energy resources (eat); this and other fundamental unconditional needs are indicated to the system by instincts, which could be described as internal sensors. Emotional signals, generated by this instinct are perceived by consciousness as “hunger”, and they activate behavioral models related to food searching and eating. In this paper we are concerned primarily with the behavior of recognition: instinctual influence on recognition modify the object-perception process (3) - (6) in such a way, that desired objects “get” enhanced recognition. It can be accomplished by modifying priors, r(h), according to the degree to which an object of type h can satisfy a particular instinct. Details of these mechanisms are not considered here, except for a specific instinct considered below.
5.7 Aesthetic emotions and instinct for knowledge.
Recognizing objects in the environment and understanding their meaning is so important for human evolutionary success that there has evolved an instinct for learning and improving concept-models. This instinct (for knowledge and learning) is described in MFT by maximization of similarity between the models and the world, (1). Emotions related to satisfaction-dissatisfaction of this instinct are perceived by us as harmony-disharmony (between our understanding of how things ought to be and how they actually are in the surrounding world). According to Kant (1790) these are aesthetic emotions (emotions that are not related directly to satisfaction or dissatisfaction of bodily needs).
Intuitionincludes an intuitive perception (imagination) of object-models and their relationships with objects in the world, as well as higher-level models of relationships among simpler models. Intuition involves fuzzy unconscious concept-models, which are in a state of being learned and being adapted toward crisp and conscious models (a theory); such models may satisfy or dissatisfy the knowledge instinct in varying degrees before they are accessible to consciousness, hence the complex emotional feel of an intuition. The beauty of a physical theory discussed often by physicists is related to satisfying our feeling of purpose in the world, that is, satisfying our need to improve the models of the meaning in our understanding of the universe.
Beauty. Harmony is an elementary aesthetic emotion related to improvement of object-models. Higher aesthetic emotions are related to the development of more complex “higher” models: we perceive an object or situation as aesthetically pleasing if it satisfies our learning instinct, that is the need for improving the models and increasing similarity (1). The highest forms of aesthetic emotion are related to the most general and most important models. According to Kantian analysis, among the highest models are models of the meaning of our existence, of our purposiveness or intentionality, and beauty is related to improving these models: we perceive an object or a situation as beautiful, when it stimulates improvement of these highest models of meaning. Beautiful is what “reminds” us of our purposiveness.
5.9 Theory testing and future directions.
The general neural mechanisms of the elementary thought process, which includes neural mechanisms for bottom-up (sensory) signals, top-down “imagination” model-signals, and the resonant matching between the two (Grossberg 1988; Zeki 1993; Freeman 1975), have been confirmed by neural and psychological experiments (these mechanisms are similar in MFT and ART, Carpenter and Grossberg, 1987). Adaptive modeling abilities are well studied and adaptive parameters have been identified with synaptic connections (Koch and Segev 1998; Hebb 1949); instinctual learning mechanisms have been studied in psychology and linguistics (Piaget 2000; Chomsky 1981). Ongoing and future research will confirm, disprove, or suggest modifications to specific mechanisms of model parameterization and parameter adaptation (5) or (8), reduction of fuzziness during learning (9), similarity measure (1) as a foundation of aesthetic instinct for knowledge, relationships between psychological and neural mechanisms of learning on the one hand and, on the other, aesthetic feelings of harmony and emotion of beautiful. Differentiated forms of (1) need to be developed for various forms of the knowledge instinct (child development, language learning, etc.) Future experimental research needs to study in details the nature of hierarchical interactions: to what extent the hierarchy is “hardwired” vs. adaptively emerging; what is a hierarchy of learning instinct? A theory of emerging hierarchical models will have to be developed (that is, adaptive, dynamic, fuzzy hierarchy- heterarchy).
5.10 Thinking process and semiotics
Semiotics studies processes of codification in nature (Peirce 1935-66; Taborsky, 1999); classical semiotics studied the symbol-content of culture (Sebeok 1995). This paper concentrates on processes in the mind that mediate between sensory data and concepts. For example, consider a written word "chair". It can be interpreted by a mind to refer to something else: an entity in the world, a specific chair, or the concept "chair" in the mind. In this process, the mind, or an intelligent system is called an interpreter, the written word is called a sign, the real-world chair is called a designatum, and the concept in the interpreter's mind, the internal representation of the results of interpretation is called an interpretant of the sign. The essence of a sign is that it can be interpreted by an interpreter to refer to something else, a designatum. This process of sign interpretation is an element of a more general process called semiosis, which consists of multiple processes of sign interpretation at multiple levels of the mind hierarchy.
In mathematics and in “Symbolic AI” there is no difference between signs and symbols. Both are considered as notations, arbitrary non-adaptive entities with axiomatically fixed meaning. But in general culture, symbols are understood also as psychological processes of sign interpretation. Jung emphasized that symbol-processes connect conscious and unconscious (Jung 1969), Pribram wrote of symbols as adaptive, context-sensitive signals in the brain, whereas signs he identified with less adaptive and relatively context-insensitive neural signals (Pribram 1971).
In classical and natural semiotics (Peirce 1935-66; Sebeok 1995, Morris 1971) the words sign and symbol are not used consistently; in this paper, a sign means something that can be interpreted to mean something else (like a mathematical notation, or a word), and the process of interpretation is called a symbol-process, or symbol. Interpretation, or understanding of a sign by the mind according to MFT is due to the fact that a sign (e.g., a word) is a part of an object-model (or a situation-model at higher levels of the mind hierarchy). The mechanism of a sign interpretation therefore involves first an activation of an object-model, which is connected to instincts that the object might satisfy, and also to behavioral models that can make use of this object for instinct satisfaction. Second, a sign is understood in the context of a more general situation in the next layer consisting of more general concept-models, which accepts as input-signals the results of lower-level sign recognition. That is, recognized signs comprise input signals for the next layer models, which ‘cognize’ more general concept-models.
A symbol-process of a sign interpretation coincides with an elementary thought-process. Each sign-interpretation or elementary thought process, a symbol, involves conscious and unconscious, emotions, concepts, and behavior; this definition connecting symbols to archetypes (fuzzy unconscious model-concepts) corresponds to a usage in general culture and psychology. As described previously, this process continues up and up the hierarchy of models and mind toward the most general models. In semiotics this process is called semiosis, a continuous process of creating and interpreting the world outside (and inside our mind) as an infinite hierarchical stream of signs and symbol-processes.
References
Albus, J. and A. Meystel. 2001. Engineering of the Mind: An Introduction to the Science of Intelligent Systems. New York: Wiley
AHCD. 2000. American Heritage College Dictionary. 3rd edition. Boston, MA.: Houghton Mifflin
Aristotle. IV BC. 1995. Metaphysics. In: Complete Works of Aristotle. Editor: J. Barnes. Princeton, NJ.: Princeton University Press.
Bellman, R. 1961. Adaptive Control Processes. Princeton, NJ.: Princeton University Press.
Carpenter, G.A. And Grossberg, S. 1987. A massively parallel architecture for a self-organizing neural pattern recognition machine. In: Computer Vision, Graphics and Image Processing. 37: 54-115.
Chomsky, N. 1981. In: Explanations in Linguistics. Hornstein, N. and D. Lightfoot. Eds. London: Longman.
Damasio, A. 1995. Descartes' Error: Emotion, Reason and the Human Brain. New York: Avon
Deacon, T. 1998. The Symbolic Species: The co-evolution of language and the brain. New York: Norton.
Freeman, W. 1975. Mass Action in the Nervous System. New York: Academic Press.
Grossberg, S. and Levine, D. S. 1987. Neural dynamics of attentionally modulated Pavlovian condition: blocking, inter-stimulus interval and secondary reinforcement. In: Applied Optics, 26: 5015-5030.
Grossberg, S. & Schmajuk, N.A. 1987. Neural dynamics of attentionally modulated Pavlovian conditioning: conditioned reinforcement, inhibition and opponent processing. Psychobiology, 15(3),p.195-240.
Grossberg, S. 1988. Neural Networks and natural Intelligence. Cambridge, MA.: MIT Press.
Grossberg, S. 2000. Linking mind to brain: the mathematics of biological intelligence. In: Notices of the American Mathematical Society. 471:1361-1372.
Hameroff, S. 1994. Toward a Scientific Basis for Consciousness. Cambridge, MA.: MIT Press.
Hebb, D. 1949. Organization of Behavior. New York: Wiley
Jackendoff, R. 2002. Foundations of Language: Brain, Meaning, Grammar, Evolution. Oxford: Oxford University Press.
Jang, J-S, Sun, C-T. and E. Mizutani. 1996. Neuro-Fuzzy and Soft Computing: A computational approach to learning and machine intelligence. Prentice Hall.
Josephson, B. 1997. An Integrated Theory of Nervous System Functioning embracing Nativism and Constructivism. International Complex systems Conference. Nashua, NH.: Sept 21-26.
Jung, C. (1934) 1969. Archetypes of the Collective Unconscious. In: The Collected Works. V.9,II. Bollingen Series XX, Princeton, NJ.: Princeton University Press.
Kant, I. (1790) 1914. Critique of Judgment. Tr. J.H. Bernard. London: MacMillan
Koch, C. and I. Segev. 1998. Eds. Methods in Neuronal Modeling: From Ions to networks. Cambridge, MA.: MIT Press.
Meystel, A. and J. Albus. 2001. Intelligent Systems: Architecture, Design and Control. New York: Wiley.
Meystel, A. 1995. Semiotic Modeling and Situational Analysis. Bala Cynwyd, PA.: AdRem
Minsky, M. 1988. The Society of Mind. Cambridge, MA.: MIT Press.
Morris, C. 1971. Writings on the General Theory of Signs. T.A. Sebeok. Ed. The Hague: Mouton
Newell, A. 1983. Intellectual Issues in the history of artificial intelligence. In: The Study of Information. Machlup, F. and U. Mansfield, eds. New York: Wiley.
Peirce, C.S. 1935-66. Collected Papers of Charles Sanders Peirce. Cambridge, MA.: Harvard University Press.
Penrose, R. 1994. Shadows of the Mind. Oxford: Oxford University Press.
Perlovsky, L.I. 1996b. Mathematical Concepts of Intellect. In: Proceedings, World Congress on Neural Networks. San Diego, CA.: L. Erlbaum Assoc. Pp. 1013-16.
Perlovksy, L.I. 1996a. Gödel Theorem and Semiotics. In: Proceedings of the Conference on Intelligent Systems and Semiotics '96. Gaithersburg, MD. V. 2: pp. 14-18.
Perlovsky, L.I. 1997. Physical Concepts of Intellect. In: Proceddings, russian Academy of Sciences, 354(3). Pp. 320-323.
Perlovsky, L. I. 1998b Cyberaesthetics: aesthetics, learning and control. STIS'98. Gaithersberg, MD.
Perlovsky, L.I. 1998a Conundrum of Combinatorial Complexity. IEEE. Trans. PAMI. 20(6): 666-70.
Perlovsky, L.I. 1999. Emotions, Learning and Control. In: Proceedings, International Symposium. Intelligent Control, Intelligent Systems and Semiotics. Cambridge, MA. Pp. 131-137.
Perlovsky, L.I. 2001. Neural Networks and Intellect: using model based concepts. New York: Oxford University Press.
Piaget, J. 2000. The Psychology of the Child. Tr. H. Weaver. New York: Basic Books
Pribram, K. 1971. Languages of the Brain. Prentice Hall.
Sebeok, T. 1995. Sign: An Introduction to Semiotics. Toronto: University of Toronto Press.
Taborsky, E. (Ed.) 1999. Semiosis.Evolution.Energy: Towards a reconceptualization of the sign. Aachen, Germany: Shaker-Verlag.
Westfall, R. 1983. Never at Rest: A Biography of Isaac Newton. Cambridge, UK: Cambridge University Press.
Zadeh, L. 1997. Information Granulation and its centrality in human and machine intelligence. In: Proceedings of the Conference on Intelligent Systems and Semiotics. '97. Gaithersburg, MD. Pp 26-30.
Zeki, S. 1993. A Vision of the Brain. Oxford, UK: Blackwell