WHAT’S GOING ON WITH THE TOPOLOGY OF RECURSION?

Donald H. McNeil

c/o Jefferson Square, 726 Washington Boulevard

Williamsport, PA 17701 USA

© This paper is not for reproduction without permission of the author(s).

ABSTRACT

The notion of “recursion” — by various definitions — goes around and about in scholarly circles, but too often without the appreciation which it deserves. Meanwhile, the quest for invariants lies at the core of human pursuits generally. This article offers a reminder about how invariance mutually entails recursion and how the topology of recursion helps to make sense of it all. Examples are drawn from mathematics, physical sciences, cybernetics, biology, and finally from the realms of the psyche and society in order to cast recursion into various perspectives. The topology of the torus is found to be ubiquitous where recursions and invariants are concerned. What counts as a “self” and what makes for “self-reference” are reconsidered, and some semiotic implications of topology are suggested.

1. INTRODUCTION

There are unconventional scholarly circles where “recursion” goes around as a compelling concept, despite the prevailing rational doctrine that everything proper must line up neatly from beginning to end. Proponents of recursive views variously refer for their exemplars to a particular computational method or to a generalized recurrence, to a simple repetition or to a complex circulation, to a cyclical order of a cyclical order or to a mysterious process of reflexive self-reference. Dictionaries define recursion generally as the recurring return of something but more particularly as the use of a repeated series of steps each based on the one before to produce a result. There is also the technical definition in computer science and mathematics which identifies recursion with an algorithmic process which obtains its results by calling “itself” as a subroutine. Examples pertaining to all of these conceptions and definitions are offered in this article. Throughout, however, it will be assumed that recursion proper involves at least one cyclical process which produces some of its results by using or referring back to some of the previous results of that same process, thus to evince a kind of “circular causality.” Along the way it will be remarked that recursions are to be found at the core of invariances and vice versa, the two together being prerequisites for selfness as a whole. Moreover, it will become apparent that it is not primarily the morphology but rather the topology of processes that serves best to enlighten our appreciation of recursion and of the spin-offs therefrom.

2. AN EXEMPLAR

Whether it be the tunes re-playing in our heads or the background beat in a shopping plaza, the sound of music keeps on keeping on. It is commercial and it is personal, agitating and soothing, anesthetizing and emotive, persistent and ubiquitous. It may resonate in melodious consonance or jangle in cacophonous dissonance, depending upon the talent of the purveyor and the ear of the listener. Music appreciation is at once cerebral and visceral and kinesthetic. The language of music includes poesy and melody in complement with the rhythms of life — moving the enchanted to sing and to dance. It can tell a story, with or without lyrics. It can be evocative, communicative, symbolic, and meaningful, hence deeply semiotic. Moreover, every performance is an interpretation, therefore richly hermeneutic. Music is made and always involves some kind of co-operation in a reciprocity of give and take. Different renditions of a tune may take excursions from the original composition even as they remain recognizably the same. Improvisations notwithstanding, a familiar refrain takes its place in culture as a relative invariant. Music comes in finite pieces yet streams on and on. Musical themes connect what might otherwise remain separate and distinguish what might otherwise be blurred. Individual musical tones — “notes” — are associated with characteristic frequencies of physical oscillations, but receive their timbre from compounded resonances and reverberations. Harmonies enrich melodies, and melodies mutually complement rhythms. Musical performance makes sense only after repetitions in practice and rehearsal, then holds its quality only so long as musicians continually adjust to minimize unwanted deviations. Music reinforces habit, paces work, exalts religion, and suffuses tradition. Whether one thinks of life as a dance or a symphony, a song or a forced march, there is no denying that reverberations of music accompany everything people do. Although some pundits would define humans as homo sapiens sapiens, we might better appreciate mankind as homo sapiens pro musica.

As the previous paragraph suggests, talk about the roles and the effects of music entails talk about persistence, repetition, convergence, correction, distinction, connection, constancy, and change. Technically it entails oscillations and vibrations; functionally it resonates with individual selves. The paradox that variations, e.g., of pitch and beat, produce invariants can resolve into a conception of how invariances may emerge from repetitions and vice versa. Music goes on by going ‘round. There is a complementarity between melody and rhythm in which both are necessary, mutually inseparable but mutually incommensurable. The logic of music is not that of the “exclusive and exhaustive” but rather of the inclusive, albeit partial. The linear appearance of written music belies that the embodiment of music in performance is recursive and interwoven in the extreme, not a hierarchy but truly a heterarchy in which centers of expression take turns in control, e.g., with various distinct themes and individual solos. A few signature notes can identify a particular piece of music as itself, even as it remains a part of all music. Profound music is richly connected within, thus the better to evoke connections and associations in both listener and performer. The characteristics of music are not alone in a reverberative topology of recursion. Music partakes of volution, invariance, resonance, heterarchy, complementarity, cybernation, connected individuation, and semiosis, themes which will be found recurring and recognizable throughout the following pages.

3. GOING AROUND

This article, around and about recursion, begins the way some say all human endeavor begins: in the quest for invariants. That invariance entails recursion is a tautology insofar as a percipient supposes something to be invariant or “absolute” if and only if it appears unchanged every time that percipient re-examines it. Formal invariants found to be “constants of mathematics” such as π (= 3.141592 ...) and e (= 2.718281 ...) hold steady, if for no other reason than that any variation which they might have is thrown away as negligible in the process of reducing them to calculations. Experimental invariants found to be “constants of Nature” such as c (the velocity of light “in a vacuum”) retain empirical invariance until someone proves otherwise. In the case of theoretical invariants taken to be “laws of physics” such as E = mv²/2 and E = mc² the formalized relationship itself is the nominal invariant which holds until it is found inaccurate, incomplete or simply wrong. In the meantime, we confidently use π as an invariant when calculating the circumference of a circle and happily refer to any of the established “laws” of physics as invariants where we think they are applicable. We may even go into a laboratory and retest for ourselves that, within a reasonable margin of experimental error, particular constants and particular laws are correct. Moreover, we may go back repeatedly to check any putative law using the invariants at the heart of the physical sciences, namely “conservation laws” of mass and energy, of linear momentum, of angular momentum, etc.

Conservation laws may be taken to be meta-laws, hence meta-invariants, in that they are empirically established generalized criteria which all particular formulations must accommodate. Our returning to meta-laws as standards itself produces a methodological recursion at the heart of Science. The quest for new invariants, new constants, and new laws continues, and old apple carts may be upset in the future as they have been in the past, but people of scientific faith proceed undaunted, taking for granted that in an otherwise restless universe Nature has provided some convenient “absolutes” for which no further explanation is needed. It is easy to forget that such faith stems from a belief instilled by recurring confirmation, by repetition, by habits, by confidence in authorities ... or perhaps by a recurring failure to notice any contrary information. Meanwhile, “ordinary Science” itself achieves its invariance as a reliable method through a conventional process of “orderly and repeatable” experiments supported by replicable measurements taken in comparison to fixed standards, i.e., business as usual except when there occur “scientific revolutions” (Kuhn 1970). As it happens, the author of the present article does believe in scientific method where it applies and in the invariants mentioned heretofore, but does not take invariances simply as “Nature’s givens,” supposing rather that they arise from the “topology of recursivity” in ways not usually appreciated. To explore this supposition, however, we must move beyond tautological recursion and relational invariance and repeatable experiments to explore some other stirring matters.

3.1 COMPUTATIONAL RECURSION AND ITERATION

For some people, recursion — sometimes identified with “reflexivity” — has been freighted with special and almost magical significance in the fields of general system(s) theory, second order cybernetics, and semiotics. For others it means nothing more than recurrence or repetition or cycling or looping. Mathematicians, especially those concerned with computation theory, staked strong claims on a particular concept of “recursion” long ago, so their definition deserves our immediate attention. In the theory of computation as enunciated by Gödel, Church, Turing, von Neumann, et al. (Hofstadter 1979), “recursion” is a repetitive process in which the result of an algorithm is specified in terms of “itself.” Recursion in this mathematical sense stands in a dual or equivalence relation with mathematical iteration which is defined to be a repetitive process in which the result of an algorithm is specified in terms other than itself, typically terms of lower order. A theorem of the theory of computation tells us that for every recursive algorithm there is an iterative algorithm which will produce the same result and vice versa. It is beyond the scope of this article to consider whether this theorem can be generalized to hold for any process of any kind in any realm whatsoever, but the reader is invited to consider the possibility.

3.2 EXPLORING THE FACTORIAL

The textbook (Davis 1958) example of a recursive algorithm is the one for calculating the “Factorial” of a number N, and it also provides a clear comparison between recursive and iterative approaches. Factorial (N) is defined to be the arithmetic product of all the integers from 1 through N, that is:

Factorial (N) = 1 x 2 x 3 x ... x N.

An iterative algorithm for this calculation takes a form similar to this definition, so a computer program to do the calculation would hold aside N, set a provisional value for the Factorial result as 1, and run a counter which begins at the value 1. The iteration, then, is to add 1 to the counter and, if the counter is not yet greater than N, multiply the provisional result by the counter and repeat, else stop and return the provisional result as the final value of Factorial (N). We note that Factorial as a mathematical entity appears nowhere within the iterative algorithm and only implicitly in the way that algorithm was designed. The meaning of “Factorial” here is quite clear and explicit, however, and closely resembles the original definition of factorialization, i.e., multiply together all the integers from 1 through N.

In contrast with an iterative approach, a recursive algorithm for the calculation of the Factorial has the form:

Factorial (N) = N x Factorial (N – 1), with Factorial (0) defined to be equal to 1.

Here the computer program to compute the factorial refers to a subroutine called “Factorial” which holds aside the received argument N, then cheerfully “calls itself” with argument (N – 1) to get the value of Factorial (N – 1) which can then be multiplied by N to return Factorial (N) as a result. Leaving aside the technical machinations which make a computer subroutine “re-enterable” and hence able to call upon itself recursively, it may appear that an algorithm fashioned in this way is getting its result from smoke and mirrors, especially mirrors. Nowhere in the recursive specification is there any semblance of the original definition of what “factorializing” means, merely an assumption that Factorial (N) = N x Factorial (N – 1), whatever Factorial (N – 1) turns out to be.

It should be obvious that both the iterative algorithm and the recursive algorithm would run on and on forever if there were no stopping criteria provided for each. In the case of the iterative algorithm, the counter is checked to be sure that it has not exceeded N, for as soon as it has, the cooking up of the result is done. In the case of the recursive algorithm, the specification that Factorial (0) = 1, itself not a recursive specification, stops the recursion by simply returning the value 1 when the calling argument (N – 1) = 0. The “recursive nest” then “unwinds,” returning to the successive callers the successive intermediate results which happen to be the factorials for the numbers from 1 through (N – 1), eventually getting back to the first caller which multiplies that net result for Factorial (N – 1) by N and spits out the final value as Factorial (N).

Among the semiotic implications of all this are that, first, the specification of an “entity” in terms of “itself” can work perfectly well without contradiction or infinite regress under the proper conditions and, second, that there may be a way in general to respecify recursivity as iterativity and vice versa. This latter, if true, would suggest that either a self-referential recursive or a constitutive iterative approach is equally effective throughout semiotics and systems, but that would require a bulky thesis to prove.

The former point deserves elaboration in the context of this article, however. Before we suppose that we have found in mathematical recursion some profound exemplar of “selfness” via formal self-reference, it is imperative to reexamine the recursive specification of the Factorial algorithm and note that it could as well have been composed of N – 1 different subroutines, i.e., Factorial_N-1, Factorial_N-2, etc., through Factorial₀, each to be called separately and applied successively, the intermediate results to be multiplied together and eventually with N to obtain the net result. Here a ghost of the iterative specification reappears, even as literal “self-reference” disappears. This is not altogether surprising, since the recursive algorithm for Factorial never did refer to itself per se but rather to earlier results calculated by a version of the same algorithm which was made to have “otherness” by technical machinations hidden in the re-enterable programming.

Thus the referred name stays the same but the computer process which effectuates it is new each time the subroutine is called. But does not “self-reference” in general necessarily refer, after all, to an “other” which has been made separate by time or distance or perspective or by an intervening process? Certainly, in the case of the “self-referential” recursive algorithm for the Factorial, there can be no doubt that each reference to “Factorial” is a call to retrieve a prospective value which will, as the recursive nest unwinds, become a previously calculated intermediate result, that is, an “other” resulting from reference to a single name but not really to a single “self.” Moreover, other putative selfness in the theory of computation, e.g., von Neumann’s reckoning about “self-reproducing automata,” involve similar differences, so “self” becomes a metaphor at best, a confusing paradox only to those who take it literally.

3.3 UNSELFISH RECURSION

Mathematical recursion without self-ish pretense certainly has important ramifications outside the theory and practice of computational algorithms. “Natural” and formal constants — such as π and e which were noted previously — are richly related to recursion, indeed in a more general way than commonly used equations and theorems might lead us to believe. But here we can find repetitive processes which invite a deeper appreciation of invariants. For example, the number 2.718281... represented by the symbol e is worthy of reflection in at least the following ways:

1. It is the “base” of the “natural” logarithms, i.e., ln (e^x) = x = e^{ln (x)}.

2. It is related recursively to all of the positive integers, since e itself can be calculated to as close an approximation as desired using the equation: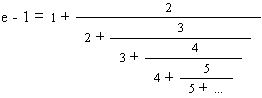

3. It is related iteratively to all of the positive integers, since e^x for any value of x can be calculated to as close an approximation as desired as: e^x = 1 + x²/2! + x³/3! + x⁴/4! + x⁵/5! + x⁶/6! + x⁷/7! + …

4. It is related to convergent infinite “power series” and to factorials (“Factorial (n)” here represented by the shorthand “n!”) as: e^x = 1 + x²/2! + x³/3! + x⁴/4! + x⁵/5! + x⁶/6! + x⁷/7! + …

5. It is related to addition, multiplication, and exponentiation because e^{x + y} = e^x x e^y.

6. It is related to the differential and integral calculus as the only mathematical function which is its own derivative to the n^th degree, i.e., dⁿ(e^x)/dxⁿ = e^x.

7. It is related as a progenitor to the circular functions of trigonometry and hence to angle, rotation, and oscillation, e.g., sin (x) = (e^ix – e^-ix)/2i.

8. It is related to complex (or “imaginary”) numbers and, again, to trigonometric functions through: e^{x + iy} = cos (x) + i sin (y).

9. It is related at once both to π of the circle and to √–1 = i through e^iπ = –1.

10. It is related to repetition, rotation, periodicity, oscillation, reverberation, and “recursion” (by some definition) in the complex analytical plane pictured on the next page.

The fact that one little invariant transcendental number e appears in so many representations and in collusion with another little invariant transcendental number π and the mysterious i = √-1 means that it resides with them at the core of circularity, both in stasis and in motion (Nehari 1961). If ever there were a symbolic sequence which offers a succinct representation of circular recurrence it would have to be:

e⁰ = 1

e^iπ/2 = i (= √–1)

e^iπ = –1

e^3iπ/2 = –i (= –√–1)

e^2iπ = 1

e^5iπ/2 = i (= √–1)

… etc.

repeating cyclically as the coefficient numbers in the exponent increase linearly. It is typically diagrammed on the “complex plane” of mathematical analysis with a horizontal axis of so-called “real” numbers and a vertical axis of so-called “imaginary” numbers as:

which further tells us that if z = e^i then

z = e^i = 1 for  = 0;

dz/d = i¹ e^i = i for  = 0;

d²z/d² = i² e^i = –1 for  = 0;

d³z/d³ = i³ e^i = –i for  = 0;

d⁴z/d⁴ = i⁴ e^i = 1 for  = 0;

d⁵z/d⁵ = i⁵ e^i = i for  = 0;

… etc.

where the effects of successive derivatives progresses counterclockwise on the complex plane in the direction of rotation indicated by the arrow … and so round and round. Clearly, from the various examples above, it is not only possible but rather commonplace for the accumulation of an “infinite” number of terms in a series or for an “endless” repetition of a simple process or for an “indefinite” monotonic increase in a simple numeric variable to induce a finite circulation or rotation, thus producing an invariant or evincing an eigenvalue attractor or making a closed form from an open-ended one, or, dare we say, carrying us from the quantitative to the qualitative realm via a stable, convergent recursion. That “exponential increase” can, by the introduction of an “imaginary” coefficient in the exponent, become “perpetual spiraling” is very consequential and perhaps somewhat reassuring. Apparently, nothing can stay around unless it is going around, even in formal mathematics.

4. CIRCULARITY AND ITS INVARIANTS

Despite doctrinaire linearities and reductivities in the formulations in the Western Rational Tradition (WRT), the commitment to repetitions and to circularity and to curl and to representations of dynamical stirrings is ubiquitous and inescapable. Moreover, at least in simple formal cases, the inextricable relationships between invariance, iteration, and recursion are evident by inspection of the relevant formulae. Thus may various paradoxes of “infinite regress” dissolve in “circular causalities” which form convergent closures. Reiteration bears repeating: even in formalisms there appear metaphorical “attractors” of stability toward which mathematical entities may tend under recursion and/or iteration and these become the eigenmarks of invariances. But formalisms in language and in mathematics are notoriously under-dimensioned shadows of what they represent. What, then, can be said of what passes for the “real world”?

4.1 GYROSCOPIC TURNINGS

At the back of the physics textbooks in the chapters which are never reached before the end of the school term there sits one of Nature’s most obvious but often underrated invariants: the gyroscopic effect. Many a child has played with a spinning top or toy gyroscope and marveled at its antics: its stubborn tendency to retain the orientation in which it was originally spun, its counter-intuitive ducking sideways rather than straight away when disturbed, and its intoxicated wobble of precession and nutation when it is “running down.” Many an adult, however, has not attended to the marvelous fact that the orientation of the axis of rotation of a well-spun gyro has an invariant orientation in the whole universe or, rather, that it acts as a relative invariant therein, since it can under coercion be disturbed, reoriented or stopped altogether.

One reason that lessons about gyros are left until the last or the never in ordinary pedagogical situations is that the calculations about them are very difficult, involving differential vector calculus together with some seemingly gratuitous approximations and occasional fudge factors. Nonetheless, “center of mass,” “moment of inertia,” “torque,” and “angular momentum” — this lattermost having formerly been called “action” in classical physics and by whatever name recognized as being “conserved” — are all at work whenever and wherever any mass or energy stirs, spins, rotates or follows a curved path. In other words, any turning movement of the stuff of physics entails a relative invariant of angular momentum which is measured perpendicular to the plane of the turning as a pseudo-vector called “curl”. However partial or tiny or temporary it may be, every gyroscopic motion somehow partakes of the total angular momentum in the whole “system” of rotating entities under consideration and acts so as to conserve the sum of that “action.” Repetition, reverberation, re-volution, and rotation are all at stake in this stirring dance, and so, we must surmise, is recursion by any reasonable definition. The “self” at stake is the mass on an axis, and the invariance of its rotational repetition is an implicit “self-reference.” As in the case of a recursive algorithm, the gyrating “self” becomes objectified as a sequence of “others” by references to previous outcomes, in this case by the timing of rotation and hence by references to the successive physically embodied angular positions. There can be no doubt that the well-spun gyro has a relatively invariant individuality of orientation which transcends its manifest construction as a material object. It is the recursion of its persistent turning which makes this so.

4.2 CYBERNETIC CIRCUITS

Invariants and their mutually entailed recursions have profound embodied manifestations in processes. For systemists and cyberneticians the “feedback loop” is a salient prototype. Whenever and wherever there is a connection of the output of any process directly or indirectly back to its input, a cybernetic circuit is established. Of all the innumerable looping connections which can be made, only a relatively few of them have the potential to reach a “dynamic equilibrium” or “steady state” or “homeostasis” depending upon the actual processes involved, their physical interconnections, their timings, and their surroundings. The circulation in a cybernetic loop may be physical, electrical, fluidic, pneumatic, chemical, computational, biological, psychological, and even social, e.g., through communications, and any combination thereof. The criteria for dynamic equilibrium in cybernetic loops are very technical and rather strict. (Note: Because cyclical progressions are entailed, the “complex plane,” complete with e and π and i as previously mentioned, is a key to performing the engineering calculations regarding the stability of cybernetic loops.)

Most interconnected loops of processes are unstable, having a tendency to explode or to collapse if left to themselves. Of course, exploding and collapsing may be slow relative to the resolving power of any given percipient, so the illusion that a particular feedback network is stable may persist for relatively long periods in human terms, only to provide a surprise later. Then, too, a cybernation which is nominally stable may undergo changes within or from without which make it quite unstable and, again, a surprise may ensue. With all the vagaries of cybernetic circuits embodied in action, it may seem unlikely that any of them can be depended upon, but Murphy was wrong — else none of us would be here to quote his fallacious law — so manifest cybernetics does exhibit very many dynamic stabilities, that is to say, relative invariances. If this were not true, nothing would persist long enough to perceive or to be perceived. Thus, as with the spinning gyro, a circulating, “self-corrective,” dynamically stable feedback loop manifests itself as a relative invariant. Unlike an unpowered gyro which is a relatively passive invariant, however, a powered cybernetic loop is relatively active in preserving its invariance. Within certain bounds, it will react — more or less counter-intuitively — to external disturbances and persist in its persistence. When perturbed beyond its range of dynamic stability, it tends not simply to break down immediately but rather first to oscillate madly in an attempt to recover stability before it finally collapses precipitously. Alternatively, it may change its modality and persist in a modified form. In any case, while it lasts, dynamic stability in cybernation “fights” to persist in such a way as to appear to be a purpose-driven self. The harder it is pushed to deviate the harder it pushes back, hence the notorious difficulty of changing any established system.

A cybernetic entity may be man-made or may occur “naturally.” Every physical entity, every living creature, every ecosystem, and every lasting social order entails uncountable numbers of cybernetic loops, some of which are highly stable but many of which are transitory, fluctuating, re-centering in different modalities, changing in their connectivities, reorganizing internally, and perhaps dispersing, only to reappear in spin-offs and reconfigurations. Just as the toy gyroscope is a prototype for invariants of gyration, so a household thermostatically controlled air conditioner is a prototype for elementary cybernation. Once a desired temperature is set by an external agent, departures from that temperature are sensed by the thermostat and the air conditioning is adjusted: temperature too high leads to cooler conditioned air and temperature too low leads to warmer conditioned air. Corrective action to hold the conditioned air at a relatively invariant temperature, then, is accomplished by reacting to the deviations or “errors” which are sensed in actual temperature. This scheme works as long as the air conditioning can handle the rate and magnitude of ambient variations, but it fails outside its range of stability, e.g., if the house burns down around it. Such “closed loop” or “circular causality” or “feedback control” is operative to a greater or lesser degree always and everywhere that there is a loop of effects, whether or not it is noticed or appreciated, so we can say with Gregory Bateson that “all processes are circular” after all. Furthermore, nothing cybernetic can stay steady without recursive reverberations, deviations, and excursions, for it is circulating changes that keep cybernations relatively invariant.

4.3 MODELS OF CYBERNATION FOR RELATIVE INVARIANCE

A simple feedback loop construed cybernetically can be pictured as:

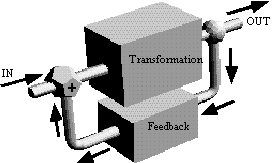
The obvious recursion, i.e., coursing around, of the flow at the core of the loop is mirrored in the formal equation which engineers often write for the throughput of the whole circuit, to wit:

OUT = (OUT x Feedback + IN) x Transformation

which is nominally a self-referential recursive formulation in terms of “OUT,” though, of course, the “OUT” on the left side of the equation is not really the “OUT” on the right side of the equation but rather a later “OUT,” a successor version of “itself.” Nonetheless this so-called “feedback equation” is typically taken literally and by simple algebra rewritten into the non-recursive form:

OUT = (IN x Transformation) / (1 – Transformation x Feedback)

from which many engineering calculations can be made, e.g., using the calculus of Laplace transforms, as long as the connectivity of the loop remains unchanged and both the Transformation and the Feedback remain constant, i.e., invariant. In the “real world” where such linearity and constancy are rare outside a laboratory setting and where very elaborate networks of feedback loops are common, calculations become much more difficult, typically requiring a computer simulation which employs recursive and/or iterative algorithms to obtain results, together with more than a little engineering artfulness.

Theoretical appreciation of feedback cybernation and the criteria for its dynamic stability is commonly identified with the work of mathematician Norbert Wiener and his colleagues in the 1940s (Wiener 1948). Long before that era, however, practical applications of feedback control were manifest, e.g., in James Watt’s intuitively-designed spinning governor for the steam engine and in James Clerk Maxwell’s mathematically-derived theory for it which was formulated retrospectively. Still earlier there were intuitive appreciations of “steersmanship” and closed loop control through circular causality, but despite the distinguished history of cybernation there is remarkably little educated appreciation of it in the cultures of the WRT today. Attempts by “management cyberneticians” to enlighten a wider audience of adults (Senge 1990; Clemson 1984) pass as fads, and children get no lessons about what makes things go on. We might think otherwise in a world full of thermostats and automatic pilots and cruise controls, but unless one has occasion to study “control systems engineering” or another formal cybernetic discipline (Beer 1966; Del Toro and Parker 1960), the “open loop” linear model of stimulus-and-response or action-and-reaction or cause-and-effect, i.e., the loop in the illustration above with its “Feedback” connection deleted, is the dominant model in the prevailing culture of the WRT. For this naïve “zero^th order cybernetics” of simple “cause-and-effect” the feedback equation reduces to

OUT = IN x Transformation

which has the form of the equations of classical physics, e.g., Force = mass x acceleration, and so seems familiar, “obvious,” and consistent with linear causality. What is forgotten in this simplification is that a “Feedback” closure is implicit in every “open loop,” if not in the mechanism at hand then certainly in the human activities which manipulate “IN” after having observed a previous “OUT.” Circular causality is ineluctable in any instance of persistence and regulation and control, whether it be acknowledged and appreciated or not. Whether the resulting relative invariant be designated a “vicious” or a “virtuous” cycle is a matter of interpretation. In any event, goings on can’t not be cybernetic, and nothing can stay in the picture without its curls.

4.4 ENTITATIONS OUT OF RECURSIONS

Potent though it is, cybernation does not stand alone as a progenitor of eternal verities. Where the forces of gyroscopics and cybernetics combine in peculiar ways, e.g., in turbulent fluidic media, vortices and eddies and whirlpools may form. It is the rare case that such an entity forms fully and persists — Dorothy is not spun out of Kansas very often — but when and where it occurs we do tend to notice the results. A fierce tornado, a powerful hurricane, or even a weak “low pressure system” reminds us that a stable eddy may be a rarity but is nonetheless a relative invariant with impact on anything in its path. Obviously such an invariance is of the order of existence itself, for its very being depends upon turbulence and recursing change. It may move along as a whole in a lateral course from place to place, but its entitation is the result of circulations both around and through its core, i.e., of currents and cross-currents. Its wholeness is round and about its hole. We can say of the eddy here — as Heraclitus is said to have said (Haxton 2001) — that “It rests by changing,” and, moreover, that “the eddy is the entity.” (McNeil 1996) This “thing” is a true emergence, not merely in but also of the ambient media itself. In the realm of meteorological eddies which we can observe, e.g., from a satellite perspective, a hurricane might appear grossly simplified as sketched below.

Here we notice that the feedback loops and the gyroscopic curlings of a hurricane include coursings through its central core — the “eye” — as well as around that core in its gale. In other words, there are at least two mutually complementary orders of recursion, going on by going around, holding each other together because of their mutual stirrings.

Formulations and calculations related to a relatively stable hurricane are not only beyond the scope of this article but also somewhat intractable to the meteorological science which we have today. Nevertheless we notice the emergence of such an entity over an ocean, identify it by an assigned a name, and track its lateral course until it disperses. It is a relative invariant while it lasts, a persistent entity out of an eddy. It arises from no-thing and returns to no-thing, but if it runs into us with its full force, its existence and its effects are palpable. Even at a safe distance, then, a hurricane is a semiotic as well as a physical phenomenon. This primitive dynamical self, a recursion of mutual complements emergent from turbulence, is taken in this article to be a meteorological prototype for the topology of relative invariance.

4.5 AND SO ON

A complete exploration of recursions and invariants throughout the physical sciences would have to include many another class of phenomena. Most obvious of these would be electrical circuits and magnetic fields which, as described by Maxwell’s equations, are paragons of recursivity. Everyone “knows” that the “lines of force” of a magnetic field, e.g., of a bar magnet as a core, curl around between a “north” pole and a “south” pole. Furthermore, an electrical circuit is just what its name says it is, a more or less complicated network of loops about which engineers speak in terms of “circuit topologies.” Moreover, electrical and magnetic fluxes always act as mutual complements in concert with one another. The additional fact that even the simplest electro-magnetic circuits are inherently cybernetic is not ordinarily discussed as such, but clearly the “transients” and “instabilities” in circuits provide evidence of feedback effects throughout.

One cannot depart the subject of the recursions inherent in the physical sciences, however, without mentioning the goings on which are apparent in ordinary chemistry. Even the simplest chemical reactions which we conceive such as the one expressed by an “equation” for water:

H₂O = H⁺ + OH^–

signify dynamic equilibria, and the “=” sign in such equations stands for a coursing back and forth in any particular situation, in this case between bonded molecules of water and roaming ions, so at the molecular level water is a relative invariant outcome of recursing processes. Organic chemistry elaborates upon such phenomena to provide an uncounted number of chemical processes whose recursions and fluxes are richly intermingled. The relatively invariant grand respiration-transpiration cycle between animals and plants is an obvious example with an oxidation-reduction cycle at its core.

5. INTERLUDE

Beyond the mathematical formalisms and the physical sciences, recursivity acts and invariances emerge throughout the realms which we call biological and ecological and psychological and sociological. Before examining a few of these ramifications, it is important to take an interlude for perspective. The perspective suggested by the examples already explored is that of topology, in particular the topology of recursions and of invariances. We have observed that the dynamical embodiment of a hurricane taken as a whole has the general form of a bagel, i.e., the topology of a simple torus. A three dimensional perspective of a simple cybernetic loop has that topology also, as does the envelope of a gyro where a mass rotates around an axis. The question of whether a toroidal topology can be educed from considerations of formal recursion and algorithmic “self-reference” is far beyond the scope of this article, except to say that the interpretive mechanism for a recursive algorithm may be said to trace a toroidal spiraling in “computational space,” even as an iteration traces a toroidal looping. In any event, we may better appreciate the less exact sciences in flexible terms which are not so tied to morphological rigor as the models used in the physical sciences usually are, and topology can provide just the flexibility we need.

Topology is the study of continuity and closeness, where proximity and placement are considered not in terms of geometric distances or morphological shapings but rather in terms of connectivity and other properties which remain unchanged regardless of continuous transformations (Firby and Gardiner 1991; Barr 1964). Surface topology — sometimes called “rubber sheet geometry” — is primarily concerned with topological characteristics of surfaces constructed by curling a plane around into various closed formations. As a mathematical discipline, topology can be and usually is encrypted into rather incomprehensible symbolic formulations, but where authors such as Firby or Barr condescend to illustrate their texts and relate the findings of topologists to visualizable embodiments, even the layman can glean some benefits. A key theorem in surface topology is that there are four and only four kinds of closed surfaces which can be constructed by curving a plane in different ways and then sealing together the proximate edges point-for-point. These four closed surfaces are called respectively the sphere, the torus, the Klein bottle, and the projective plane and are illustrated below as their shadows may appear in two dimensions:

5.1 STRANGE SURFACES

In the topological menagerie, the sphere and the torus can be realized in the three dimensions of “ordinary space,” but the Klein bottle and the projective plane cannot be constructed in less than four dimensions because to do so would require that their surfaces pass through themselves in a way which is not topologically permitted. The Klein bottle — which can be constructed from a Möbius strip whose single edge has been sewed together all the way around — is often drawn in a two dimensional picture as above which makes it appear to have a “neck” which passes through its “body,” but a topologically correct interpretation of the Klein bottle tells us that its “neck” passes beside its “body,” thence to reconnect in no less than four dimensions. Therefore, whatever “self-reference” a Klein bottle may represent, it is not the result of any self-intersection. The projective plane is even more mysterious to our three-dimensional visualizations. It has a singularity which, as its name implies, can be interpreted as playing the role of the vanishing point for a generalized visual perspective. Topologically the Klein bottle and the projective plane are “non-orientable” surfaces, that is, they have only one side, hence no inside or outside. This and other bizarre properties of these two topologies make them prone to misinterpretations. What can best be said about them is that they highlight the fact that surface topology is about transformations as much or more than it is about entities per se. For example, a Klein bottle represents a transformation which can, among other things, turn a three dimensional object inside out, and a projective plane may be construed as a transformation related to visual perception. There is no doubt that Klein bottles and projective planes have semiotic import, but it remains for someone to develop their potentials properly as regards the topology of meaning (Flett and McNeil 1995), and no such project will be undertaken here. We should note, however, that regardless of how convincingly their shadows in less than four dimensions may be drawn to suggest otherwise, neither the Klein bottle nor the projective plane slice through themselves; and, furthermore, neither can “contain” anything, since neither has an inside or an outside. Our ordinary interpretations of the interpenetration of closed surfaces and of physical bodies and of the partitioning of any real or conceptual space do not apply with reference to non-orientable surfaces such as these, so attempts to attribute meaning to “kleinforms” (Ryan 1993) or to their putative self-intersections are fraught with dangers, but see also the articles by Rosen and by Ryan in this issue of SEED.

5.2 THE SPHERE

What can be said with intuitive as well as mathematical credibility is that spheroids and toroids and their respective transformations are ubiquitous in the embodiments which we perceive and in the representations which we use. The metaphor of the sphere dominates worldviews in the WRT where it draws emphasis to isolation, symmetry, encapsulation, exclusion, particulation, stasis, and separation. A few salient topological characteristics of the generalized sphere are:

1. It is an “orientable” surface which sets apart an inside and an outside;

2. It is inherently symmetrical;

3. It is a “simply connected” surface upon which there is only one kind of shortest line which can be drawn between any two points, namely an arc of a great circle;

4. It has a topological connectivity of four, i.e., no more than four points upon its surface can be connected, each to all others, without a connection crossing one or more of the other connections (a property which it shares with a plane surface);

5. It has a net curvature of positive 2π over its entire surface, i.e., it is convex;

6. It represents a single or first order enclosure, i.e., all circles drawn upon it can be stretched or shrunk and turned so as to be equivalent to one another;

7. If undistorted it has no orientation as a whole because it is inherently symmetrical.

We should note that all spheroids are “homeomorphic,” i.e., topologically equivalent, to each other, since size and shape and deformation do not matter to the topologist. For example, all of the figures below are topologically equivalent spheroids:

Thus sphericity is a kind of topological invariant. Because the sphere is so familiar and so dominant a paradigm in the WRT, no more need be said about it here.

5.3 THE TORUS

The torus is remarkably different from the sphere. It gets some confabulatory praise in talk of rings and of mandalas and, occasionally, of real or metaphorical donuts such as in off-handed references to Nature as “a box of bagels” in an odd text on ecology (Allen and Hoekstra 1992), but it is seldom recognized for what it is: ubiquitous wherever persistent dynamics and recurrent processes are embodied, i.e., everywhere and anyhow and always. Metaphors fitting to the torus are those of coupling, asymmetry, embrace, inclusion, vorticulation, circulation, and connection.

A simple torus may be generated by rotating a closed plane figure, e.g., a circle, around an axis as illustrated at left below:

Alternatively, one may visualize a simple torus as the envelope around a recurring path of movement, which path does not necessarily repeat itself exactly on every revolution but nonetheless has limited excursions in its cycles as suggested by the meandering line at right above. Topologists think of a simple torus as being the result of a two phase transformation constructed by curling a plane into a tube and then curling the tube to connect the open ends as suggested by the sequence of transformations below:

One can also see the torus as the envelope of the revolution of an object around a center, e.g., as the envelope of a planet’s movement around the sun, and as the topology of a cybernetic feedback loop and as the overall configuration of a hurricane or tornado and as an animal’s embodiment around its alimentary canal. A wheel is a torus and so is a compact disk and a pipe. Sieves and nets and screens are toroidal too. It is not an accident that the torus is manifest ubiquitously in natural formations and in artifacts alike for reasons which will become increasingly apparent in the remainder of this article.

Referring back to the first image defining the torus above, we shall designate as “annular” any tracing which circles the hole but does not pass through it, e.g., along the curve with the arrowhead on it, and as “meridial” any tracing such as the circle which passes through the hole but not around it. The annular and the meridial are quintessential complements, mutual and inseparable for conception and appreciation of the torus. Moreover, since they are not simply connected, annular and meridial complementary orders may be incommensurable and yet co-operate without clashing.

Armed with the images and definitions presented so far, we can begin to appreciate a few salient topological characteristics of the generalized torus such as:

1. It is an “orientable” surface which sets apart an inside and an outside.

2. Although it is symmetrical in several aspects, its overall symmetry is “broken” by at least one hole, so it is inherently asymmetrical.

3. It is “not simply connected,” having at least two kinds of shortest lines which can be drawn between any two points upon its surface, namely an annular arc around the hole and also a meridial arc through the hole.

4. A simple torus having one hole has a topological connectivity of seven, i.e., up to seven points upon its surface can be connected, each to all others, without any connection crossing any of the others, and more holes allow for more nonintersecting connections, increasing indefinitely.

5. A simple torus has a net curvature of 0 over its entire surface, i.e., it is neither convex nor concave as a whole, and each additional hole decreases its curvature by 2π, thus to yield a net negative curvature for concavity;

6. A simple torus represents a second (cyclical) order construct, i.e., having one annular cyclical ordering complementing one meridial cyclical ordering.

7. An undistorted simple torus has an orientation as a whole along an axis through its hole due to its inherent asymmetry.

8. Beyond the annular and the meridial orders there is a “Villacreaux” or re-spiratory order having chirality leftwise or rightwise which can be traced upon a torus.

Every torus which has a given number of holes is topologically equivalent to every other which has the same number of holes, since size and shape and deformation of a figure do not matter to the topologist. All of the figures below are therefore “homeomorphic,” i.e., topologically equivalent tori, each having one hole. In other words, surface topology is invariant to continuous “morphing.”

The number of holes in a torus is called its genus. Genus is a topological invariant of any particular toroid, and the equivalence of genus to the cardinality of natural numbers should be apparent. The illustration at below shows a toroid of genus nine:

Note that the sphere, having no holes, can be said to be a torus of genus zero and can enter into topological accounting as such.

6. GENERALIZING ABOUT THE TORUS

Having surveyed the salient features of the realizable topologies embodied in the sphere and the torus, we can now appreciate that all of the recursions addressed in the first portion of this article have the topological characteristics of toroids. Topological invariants such as genus can be seen to correspond to recursive relative invariants such as persistent circulations around open centers. Topological characteristics such as annular and meridial “connectivity” may serve as a felicitous model for those people who identify recursion proper with “an order of an order” and therefore find the “not simply connected” characteristic of the torus to be especially meaningful. People who take “symmetry-breaking” as a key to semiotics have much to gain in the toroidal hole, for it is the most rudimentary of the invariant marks which can be made by a circulating process, i.e., the toroidal hole is the mark of the toroidal whole. If a sphere, which has no holes, can be said to represent absence of any topological marks, then a simple torus can be said to represent one single mark and toroids of higher genus can represent an arbitrary number of marks. Topological marks tend to be less ambiguous and less volatile than, say, the writing upon a surface or any other superficial marking would be; and since a toroidal surface is its own inherent mark, it remains indelible and invariant regardless of its morphology as long as its topology remains unchanged. Since anything which can be represented can be represented by a Gödel number and any number can be represented by a toroid of appropriate genus, the attributions of embodied topological markings can be whatever we want to make of them.

6.1 THE ANNULAR AND THE MERIDIAL

The annular and the meridial turnings around a torus are inseparable constitutive complements, but they can be teased apart as in the illustration below, then recombined to compose the whole.

It is apparent by inspection of the rightmost figure above that upon the whole torus every point partakes of at least two kinds of orderings, the annular and the meridial. This at once implies heterarchy and multi-connectivity, and this is how it happens that, unlike planar and spherical models, toroidal models cannot be reduced to simple hierarchies or single optima (McCulloch 1943). Metaphors about any putative “union of opposites” (Sabelli 1989) become pale and under-dimensioned shadows beside the much richer metaphor of the torus as a “union of complements” (Jaros and McNeil 1996). Thus many an “either/or” paradox may dissolve into a “both-and” reconciliation through use of topologically sound toroidal models. Whether the annular and the meridial complements help us to bridge the “analog/digital” divide (Wilden 1980) or to comprehend such semiotic concepts as “dual coding” (Hoffmeyer 1993) is left for the reader to decide. Certainly the metaphor of prehension or grasp can be embodied as suggested by the figure at left below, and perhaps the proper places of “semiotic branchings” and “hermeneutic spirals” can be found in a figure such as the one at the right below.

For now, a thoroughgoing exploration of the semiotics embodied by the torus must await a treatise devoted to the “topology of meaning” (Flett and McNeil 1995).

6.2 THE RE-SPIRATING TRACE

Speaking of spirals, a Villacreaux tracing upon a simple torus embraces both the annular and the meridial in one continuous looping. The simplest such tracing embraces each order only once as at left below. Where more turns are taken, one can perceive a “re-spiratory” tracing such as in the example at right below.

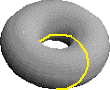
It is apparent by inspection that any particular spiral in three dimensions must be a piece of just such a fully evolved re-spiration, whereupon continuous travel along the tracing in one direction goes around and through and returns upon itself, moving from the center successively upward and outward, then outward and downward, downward and inward, then inward and upward, hence back to the center, thus to embody a living, breathing metaphor. An appreciation of the re-spiratory toroidal trace provides some alternative ways to think about reverberations in three dimensions. It may also be used to supplant under-dimensioned oscillatory models in physical sciences as well as jagged dualistic paradigms in philosophy, e.g., “the dialectic” which may turn out to be only a shadow of a spiraling process of discourse. In any event, a re-spiratory torus in perspective suggests a metaphor for the fact that the spiraling “onward and upward” of anything can easily be followed by “going over the top” into a “downward spiral” in a very natural way, even where there is a steady progression through time, e.g., “economic cycles.”

6.3 KNOTTING AND MORE

Much more follows from an appreciation of the topological characteristics of toroids than can be recounted here, but a few more hints deserve mention. If we were to re-cast our WRT metaphors of partitioning, e.g., of concepts and categories, into a toroidal rather than spherical or planar topology, the seven-fold associated with the connectivity upon the simple torus could supplant the four-fold associated with the connectivity upon the sphere or plane surface so as to elaborate our worldviews beyond doctrinaire Cartesianism. Moreover, if we let the torus become knotted, whole worlds of alternative means for representation are opened (Kauffman 1991). For example, a knot such as the one below happens to be homeomorphic to a simple torus but represents a richer kind of ordering.

Eventually, somewhere far beyond the scope of this article, we could wax meta-topological, allowing for emergences and dispersals of volutionary entities, nested recursions, throughputs, spin-offs, interpenetrations, weaves, braids, twists, and dynamical reconnections in a turbulence of currents and cross-currents where streamings mingle and eddies can’t not form. Even in this limited article it is necessary to leave the surface of surface topology to consider embodiments, contents, forms, functions, systems, and perspectives. Traces upon surfaces can be expanded into toroidal tubes, thus to add dimensionality where appropriate.

Speaking philosophically, we can say that wherever there is a turning of a turning, a going around of a going around, a curl of a curl, a rotation of a rotation, an ordering of an ordering (McNeil 1996), a regulation of a regulation (after Francisco Varela), a coordination of coordination (Maturana 1992), ideas of ideas (after Spinoza via Damasio 2003: 215), method of methods (after C.S. Peirce), communication of communication (von Foerster 1995), a law about laws (Weinberg 1975 after Kenneth Boulding), a difference that makes a difference (Bateson 1979), or, as it turns out, any web or network whatsoever there will be intrinsic toroidality, whether manifest as a relatively static structure or in the dynamics of processes. Every one of these references could be elaborated at length as richly relevant to the context of this article, but the one from Damasio is especially telling because it suggests that “the most basic kind of self is an idea, a second order idea.” Surely the only limit to appreciating the dynamic topology of life and of thought is human imagination.

7. GOING ON

The world, some wise man has said, is not partitioned the way the academic departments of a university are, but it is convenient here to proceed as if there really were some useful distinctions beyond the physical sciences among biology, ecology, psychology, and sociology as a progression which finally embraces all that Science claims to know about what is going on.

7.1 AS FOR BIOLOGY

Biology plays a pivotal role, being not so “objective” as the physical sciences and not so “subjective” as the social sciences, though necessarily partaking of them all. Recursing behaviors are biologically ubiquitous from the gross cycles of sleeping, feeding, and breeding through to the subtleties of the recursing life of an individual cell. The “topology of biology” is not a typical undergraduate course, but it is surely not the worst subject matter to reconsider early and often. Indeed, prototypes for toroidal manifestations are readily to be seen by the inspection of biological features. One of these is the toroidality of the gross anatomy of every animal which has an alimentary canal, and, of course, there are many other toroidal topologies evident in animals, e.g., the high genus closed branchings of circulatory systems and nervous systems. Nonetheless, it is the living tree such as sketched in the figure below that offers a fitting prototype for the topology of biological processes:

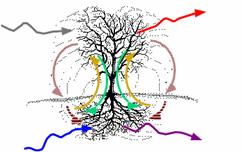
The tree stands as a whole process which is toroidal around the wooden hole of its trunk, suffused in ambient circulations and profuse with inner processes which are connected into intricate recursive feedback interrelationships. The physical structure of the branches — or of the roots — of a tree is often taken by systemists and others preoccupied with morphology as proof positive that “hierarchy is fundamental.” From a topological perspective, however, such brachiations, taken apart, are only instrumental croppings of the whole and constitute only a portion of the story of channeling and processing and recursion evinced by a living plant. Partiality to croppings of toroidal wholes can lead to narrowly focused academic researches into hierarchies and spirals and simply-connected geometrical forms and to losing sight of the forest as well as the trees, all the while provoking disgraceful brawls at scholarly conferences. A little poetry helps here if we remember Wordsworth’s admonition that “We murder to dissect.” For viable results, we may better take the living tree whole as a dynamical self, an entity emergent from recyclical biotic processes, and a biological prototype for the recursing topology of relative invariance. Throughout the bio-tore and the eco-tore, living creatures are continually remaking themselves, e.g., most of the cells in our bodies today are not physically the same entities that they were a few months ago, and so long as we survive we live in a dynamic equilibrium of perpetual rebuilding. Systemists have generalized this notion, calling it variously “autocatalysis” or “autopoiesis” and often treating it as a self-referential paradox. Strictly speaking, since the processes involved in living metabolism are the effects of a previous self — or subsystems thereof — producing another new self using input ingredients according to its own DNA plan, the name “homeopoiesis” seems more appropriate. Whatever we call it, this exquisite process is richly toroidal with physical, electromagnetic, chemical, organic, etc., connectivities operating in complex, recursive cybernetic loops and cycles. Just so, biological recursions in elaborate toroids create and maintain living things as relative invariants for the duration of their lives.

7.2 TOWARD ECOLOGY

To take a perspective of forests as well as trees, we might begin with the simple image below where trees occupy ecological centers or holes, thus to form a natural toroid of high genus, nine in this example:

Technically, this polycentric topology is that of a “heterarchy,” having multiple loci and foci of control. By any name, the living form of this panorama is a richly interacting complex in which, beyond the internal processes of each tree, there are couplings among the trees and interconnections between all of them as well as with the ambient atmosphere, the soil, and a plethora of plants and creatures not shown in the illustration. Here the biological individuals — as toroidal holes — are at once separate and together in the collective due to the “not simply connected” nature of the topology of their habitat, and thus they easily transcend any spherical metaphor which would consign them to the role of “independent” billiard balls knocking around.

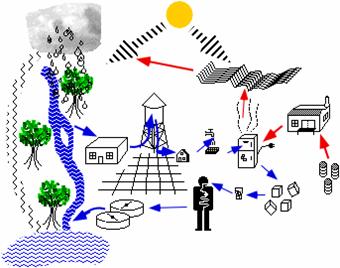
We can include more of what goes on in an ecosystem, such as human activities in the topology of ecology, as shown in the sketch below, but what matters for the purposes of this discourse is that once again a suite of interconnected recursing processes produces a relative invariant, namely the persistence of an ecosystem. Any such system is powered by the streaming through of relatively high quality energy from the Sun as a source toward the Earth as a sink. The sketch below reminds us, however, that even such “uncontrolled variables” as the Sun’s energy output to Earth may be altered in their effects by human activities, e.g., those which produce smog, ozone holes, green-housing, etc., so humans find themselves at once downstream and upstream in various of the loops, circuits, and recursions of their habitat’s cybernation. Whether the result of this over a long run is a stabilizing or de-stabilizing for the ecosystem upon which we depend is beyond human ken or computer simulation and therefore remains to be seen, but relative invariance for an indefinite duration is certainly not guaranteed. Don’t we just love surprises?

7.3 OF PSYCHOLOGY

Discourse about the human psyche — psychology — has long included words borrowed from cybernetics such as “input” and “feedback.” Determination of whether or not such words are being used appropriately and insightfully in practice is left as an exercise for the reader, but there can be no doubt that “mental stability” and “lives spiraling out of control” have at least some common sense meaning with strong cybernetic implications. The topology of mentation itself is that of reflection and re-minding. Habits, of course, are relative invariants of thought and action, stirred in the psyche and characterized by repetition. Memory produces relative invariances through recyclical processes of re-collection and re-membering while thinking is a recyclative process so powerful that it can project intentional goals as relative invariants for the future. Language is at once a relatively invariant standard for communication and a repository of evidence about the importance of recursions. The English language offers more than 200 basic words having the prefix “re-” from “react” through “revise” and then some, all of which connote persistence through recurrence. We repeat, recite, and rehearse. We recognize and represent and record and reproduce, then perhaps recollect and reflect and relate. We may reassure and resolve. We often retort and sometimes respect. And we may get lost in research or reverie. We convince ourselves and one another with reiterations and remonstrations. All the while we take ourselves for granted in our self-referential con-sciousness, which reminds us that many “co-” and “con-” words connote mutual recursivity just as the “re-” words do. Moreover, there are “volution” words which further strengthen an appreciation of turnings as in “revolution,” “involution,” “convolution,” and “evolution.” Thus do we find the “psyche-ology” in everyday conduct, thought, and language to be replete with more or less persistent relative invariants spinning from our recursing minds.

7.4 INTO SOCIOLOGY

Where two or more people interact through time, social invariants emerge. The morals and the traditions of a society, somewhat analogous to the habits of an individual, recurse and keep things going on in established ways, for better or worse. Businesses have “standards and procedures” in their corporate cultures. Governments maintain order through repeated reference to constitutions and laws, at least so long as cultures “remain stable” and things don’t “spin out of control.” With or without reference to a putative science of sociology, the interacting phases and the cycles of individual lives, of cultures, and of civilizations are matters of common experience and well-recorded history. Indeed, early sociology anticipated a process that we now call evolution, e-volution, a progressive recursive turning. In the seventeenth century, Giambattista Vico supposed that civilizations progressed through a cycle from barbarism through an age of gods, an age of heroes, an age of heroes … and back to barbarism (Bergin and Fisch 1984), and, not surprisingly, his was neither the first nor the last hypothesis about social volutionarity. All communications among people can be construed as recursive connections in a more or less volatile toroidal topology. Ultimately, any persistent way of life depends for its survival upon renewal and revitalization and refreshment and recreation and resourcefulness, all as recursing processes which keep things relatively invariant. Perhaps the strongest invariants of all in any society are the absolutes of faith and belief which bind people together in collectives in the name of religion, i.e., re-ligation, a linking back which is rich with the repetitions of ritual and tradition. Obviously, social systems can’t not express invariants throughout the topologies of their recursions.

7.5 RELATIVE ABSOLUTES

Where people reject the absolutes of conventional beliefs in favor of the radical relativism of the post-modernistic, they have, of course, merely substituted absolute relativism for relative absolutism, and in doing so they have, perhaps unwittingly, run afoul of an ostensive proof from Arthur M. Young (Young 1976) in which he shows how such relative invariants as may exist are to be found in relation to rotations and recursions, much as this article has argued. Young’s refutation of absolute relativism would proceed as follows: go outdoors on a starry night; stand and look at some stars near the horizon; turn once around in place and look back at those same stars; decide whether you rotated while the stars remained fixed or the stars rotated around you; if you conclude that the stars may have rotated around you in the few seconds it took for you to rotate in place, you are truly a radical relativist and also seriously mistaken unless Einstein was. This folksy little demonstration tells us how it happens that some things are not perceptually arbitrary or freely relative. Even the most radical constructivist has — and must have — an enduring core of reference. For everyone, regardless of philosophical persuasion, it turns out that non-coaxial rotations play the role of relative invariants or relative “absolutes.” We can say further that the more rapid the cycling of a process, i.e., the stronger the angular momentum or the cybernetic stability, etc., the stronger the invariance corresponding to it will be. Plus ça change, plus c’est la même chose!

7.6 MAKING CONNECTIONS

Clearly, sociology and psychology and ecology and biology and the -ologies of physical sciences have been made separate from one another by human design for human convenience and are at best only instrumental croppings of aspects of the topology of the whole of what we need to know. This becomes especially obvious when people invent and study reconstituted hybrids such as “the sociology of science” or “bio-physics” or “eco-cybernetics.” The misunderstandings which are produced in the WRT by educational approaches based upon jigsawed instrumental croppings of simply-connected topologies, i.e., spheres, or upon flattened and linearized and under-dimensioned Cartesian models are too numerous to count, but they do matter. Failure to see the connections, especially those of different kinds in a not simply-connected topology of comprehension, has given us alienation and conflict and no clue about alternative paradigms which might help. Here recursion and repetition and habit have not served humanity well, for more of the same no longer works. It is beyond the scope of this article to consider, but it is as important for people to know how to change stable recursions as how to appreciate them in action. Suffice it to say that where there is a relatively invariant toroidal center of attraction and recursion which is unwanted, there are meta-topological moves which can be made to obviate it, e.g., re-routing, re-connecting, and re-centering. Successful people do such things intuitively, but a lot more topological education wouldn’t hurt, so that everyone could partake of a better sense of the topology of recursion throughout the dance of life.

8. FROM HIERARCHY TO HETERARCHY

If we are bold enough to explore the topology of recursion and invariance wherever it may lead, we can find remarkable alternatives to the conventional wisdom of the WRT. For example, some traditional teachings have supposed that the grand whole of the universe is a simply-connected hierarchy with subatomic particles near the “bottom” and galaxies near the “top” while others have supposed that a universal hierarchy ascends from the back of a cosmic elephant or descends from a paternal godhead. Eventually, any discourse about simply-connected hierarchy has to stop arbitrarily in order to avoid infinite regress, refractory paradox, heresy, umbrage, profanity, and fisticuffs. There is nowadays some hope for relevant advice from physical science, however. In a physics of “superstrings,” i.e., submicroscopic toroids, “particles” are recast as “vorticles,” and wormholes in space-time make for a not-simply-connected universe, so perhaps the stage is set for physical sciences to better appreciate their own deep topologies and ours as well (Greene 1999). Meanwhile, in light of the topology of the torus, we can see through the deeply ingrained hierarchical arguments with all their paradoxes and outright contradictions by comparing two kinds of cybernetic orderings (von Foerster 1995). Let us begin with a fairly simple feedback loop which differs from the examples drawn earlier in this article by having a set point S* such as a thermostat would which establishes what output the cybernetic loop is to maintain.

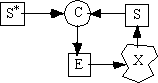
Here, X is a resultant whose condition is determined by sensor S, then compared by comparator C to the desired setting S* so that deviation can be corrected via effector E acting on X. But who sets the set point S*? If we arrange for another such loop to control this one and another to control the second one, etc., an unlimited regress of controls controlling controls is the result as illustrated below, and any invariance of X which could be established in this whole scheme would depend upon there being a reliable “prime mover” or “first cause” in the heavens somewhere above the ellipsis dots:

There is an alternative to a hierarchical ordering such as the one above, however, in an interconnection of two cybernetic loops which might together be called a holarchical ordering and which can manifest heterarchical control. It can be illustrated as follows:

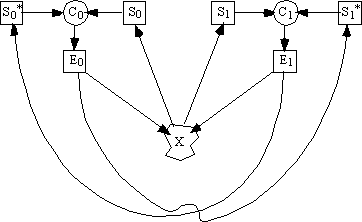
Here, the effector E₀ of loop₀ at the left adjusts not only the resultant X but also the set point of the loop₁ and vice versa, and the mutual control signals pass by each other in a toroidal topology as shown at the bottom of the diagram. Although it is certainly beyond the scope of this article to demonstrate, a properly constructed heterarchical interconnection of this kind can be stable or bistable, i.e., as a dual cybernetic loop in a toroidal order of an order which maintains dynamic equilibrium. Indeed, a “bistable multivibrator” or “flip-flop” electronic circuit is constructed in this fashion and is often employed as a computer “memory” element so as to maintain its resultant X as either a binary 0 or a binary 1, depending upon how the circuit was most recently conditioned. If we redraw the schematic of the holarchical ordering above so as to view it in a three dimensional perspective, it appears more obviously toroidal as:

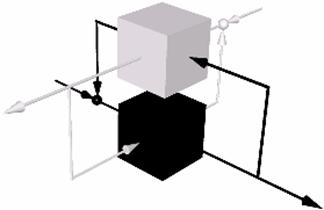
Here the one process controls the other and the other process controls the one in a patently toroidal interconnection (von Foerster 1974). The ways of nature are just so, and any locally self-controlling process must be just so as well.

9. CONCLUSION

What stays around must go around. Every persistent process is recursive and partakes of circular causality, e.g., cybernation. Where an autonomous circulating entity emerges, its realization requires at least two kinds of cyclical orders. Hence the torus with its mutually complementary annular and meridial orderings is the prototype for the topology of embodied recursion, and, insofar as recursion mutually entails invariance, for the topology of relative invariance as well. While we can say about the torus that the annular and the meridial orders complement one another in the deepest sense, we may also say that the toroidal hole and the toroidal whole implement one another in the fullest sense. They are inseparable and provide a canonical exemplar of irreducibility. The gale of the hurricane is inseparable from its “eye” just as the life of a tree is inseparable from its trunk, i.e., as the stem of a system. Although many interesting and useful meanings may be associated with other topologies such as the Klein bottle and the projective plane, we need look no farther than the torus to find recursion fully represented, invariances well established, and semiosis richly embodied. We can count on it. The metaphor of the sphere which so dominates the Western Rational Tradition is important, of course, but counts for nothing without an appreciation of the tore. It is no accident that our reflective metaphors such as “grasp” and “comprehension” are inherently toroidal. Moreover, circular logic is unavoidable, and the topology of self-reference is, after all, that of recurrent processes. Even such progressions as re-volution and e-volution turn upon themselves. Without goings around there could be nothing going on. It is through the web of dynamic, recyclical processes that our being emerges embodied as an eddy, persists as a relative invariant, reflects upon itself, construes meaning, and eventually disperses. That is what the topology of recursion is all about.

ACKNOWLEDGEMENTS

Allusions to the “topology of meaning” relate to the as yet unpublished work by R. Ian Flett of Sydney, Australia. Some of his ideas can be found, however, in (Flett and McNeil 1995) in the REFERENCES below.

During recent years I have benefited greatly from discussions with Professor R.F. Lumpp of Regis University, Denver, Colorado, particularly as regards his studies of cultural traditions and the possibility of the re-articulation of such subject matter in terms of the “topology of tradition.

This is the first article I have tried to write since 1996. It could not have been started or completed without the help and encouragement of Peter Harries-Jones of Toronto, Canada. My gratitude to him is enormous. For what you like about what you find herein, credit him; for what you dislike, blame me.

REFERENCES

Allen, Timothy F. H., and Thomas W. Hoekstra. 1992. Toward a Unified Ecology. New York: Columbia University Press.

Ashby, W. Ross. 1966. An Introduction to Cybernetics. New York: John Wiley & Sons.

Barr, Stephen. 1964. Experiments in Topology. New York: Dover.

Bateson, Gregory. 1979. Mind and Nature: A Necessary Unity. New York: Bantam Books.

Beer, Stafford. 1966. Decision and Control. New York: John Wiley & Sons.

Bergin, T.G., and M.H. Fisch. 1984. The New Science of Giambattista Vico. Ithaca: Cornell University Press.

Clemson, Barry. 1984. Cybernetics: A New Management Tool. Philadelphia: Abacus Press/Gordon and Breach Science Publishers.

Damasio, Antonio. 2003. Looking for Spinoza: Joy, Sorrow, and the Feeling Brain. New York: Harcourt, Inc.

Davis. Martin. 1958. Computability & Unsolvability. New York: McGraw-Hill.

Del Toro, Vincent, and Sydney R. Parker. 1960. Principles of Control Systems Engineering. New York: McGraw-Hill.

Firby, P.A., and C.F. Gardiner. 1991. Surface Topology. 2^nd ed., London: Ellis Horwood Ltd..

Flett, R. Ian, and Donald H. McNeil. 1995. “What’s Wrong with this Picture? Towards a Systemological Philosophy of Science with Practice.” Proceedings of the “Einstein meets Magritte” Conference, Brussels, Belgium.

Greene, Brian. 1999. The Elegant Universe. New York: W.W. Norton & Company.

Haxton, Brooks. 2001. Fragments: The Collected Wisdom of Heraclitus. New York: Viking.

Hoffmeyer, Jesper. 1993. Signs of Meaning in the Universe. Bloomington, IN: Indiana University Press.

Hofstadter, Douglas R. 1979. Gödel, Escher and Bach: An Eternal Golden Braid. New York: Basic Books.

Jaros, Gyuri G., and Donald H. McNeil. 1996. “On the Union of Complements.” Conference Proceedings of the Budapest meeting of the International Society for Systems Sciences.

Kauffman, Louis H. 1991. Knots and Physics. Singapore: World Scientific.

Kuhn, Thomas. 1970. The Structure of Scientific Revolutions. Chicago: University of Chicago Press.

Lumpp, Randolph F. 2002. Regis University, Denver, CO. Personal communications.

Maturana, Humberto, and Francesco Varela. 1992. The Tree of Knowledge. Boston: Shambhala.

McCulloch, Warren S. 1943. “A Heterarchy of Values Determined by the Topology of Nervous Nets.” Bulletin of Mathematical Biophysics. 5: 115-133.

McNeil, Donald H. 1996. “Re-framing Systemic Paradigms for the Art of Learning.” Gordon and Breach: World Futures. 46: 23-45. (Originally presented at the American Cybernetics Society conference, Philadelphia, PA, November 1993.)

Nehari, Zeev. 1961. Introduction to Complex Analysis. Boston: Allyn and Bacon.

Ryan, Paul. 1993. Video Mind, Earth Mind — Art, Communications and Ecology. New York: Peter Lang.

Sabelli, Hector C. 1989. Union of Opposites. Lawrenceville, VA: Brunswick Publishing Corporation.

Scarborough, James B. 1958. The Gyroscope - Theory and Applications. New York: Interscience.

Senge, Peter M. 1990. The Fifth Discipline: The Art & Practice of the Learning Organization. New York: Doubleday.

Von Foerster, Heinz. 1974. “Cybernetics of Epistemology.” Proceedings of the 5th Congress of the Deutsche Gesellschaft fur Kybernetik.

Von Foerster, Heinz, ed. 1995. Cybernetics of Cybernetics. 2^nd ed.., Minneapolis: Future Systems, Inc..

Weinberg, Gerald M. 1975. An Introduction to General Systems Thinking. New York: John Wiley & Sons.

Wiener, Norbert. 1948. Cybernetics. Cambridge: MIT Press.

Wilden, Anthony. 1980. System and Structure: Essays in Communication and Exchange. New York: Methuen (Tavistock Publications).

Young, Arthur M. 1976. The Geometry of Meaning. New York: Delacorte Press.

Young, Arthur M. 1976. The Reflexive Universe. New York: Delacorte Press.