What is Radical Recursion?
Steven M. Rosen
Departments of Psychology and Philosophy (Emeritus)
College of Staten Island/City
©This paper is not for reproduction without permission of the author.
ABSTRACT
Recursion or self-reference is a key feature of contemporary research and writing in semiotics. The paper commences by focusing on the role of recursion in poststructuralism. It is suggested that much of what passes for recursion in this field is in fact not recursive all the way down. After the paradoxical meaning of radical recursion is adumbrated, topology is employed to provide some examples. The properties of the Moebius strip prove helpful in bringing out the dialectical nature of radical recursion. The Moebius is employed to explore the recursive interplay of terms that are classically regarded as binary opposites: identity and difference, object and subject, continuity and discontinuity, etc. To realize radical recursion in an even more concrete manner, a higher-dimensional counterpart of the Moebius strip is utilized, namely, the Klein bottle. The presentation concludes by enlisting phenomenological philosopher Maurice Merleau-Ponty’s concept of depth to interpret the Klein bottle’s extra dimension.
1. SEMIOTICS, POSTSTRUCTURALISM, AND RECURSION
In classical signification, the stability of the relationship between the signifier and what it signifies is maintained by preserving the anonymity of the former. Attention is fixed solely on the meanings that are signified, not on the act of signification itself. With the advent of semiotics this changes. Semiotics is the discipline that studies the process of signification. Here the sign becomes recursive; instead of focusing exclusively on signified meanings, it comes to focus on itself. The signifier, which had played a predominantly tacit role in classical semiosis, is now itself explicitly signified.
Despite this role reversal inherent in the very existence of the discipline of semiotics, structuralist semioticians like Saussure still sought to preserve the invariance of the link between the given signifier and what it signifies. The problem is that, once classical signification is surpassed by signifying the signifier, the door is opened to an infinite regress. For now, it seems that no signifier is exempted from mutation into that which is signified. A new signifier is presumably needed to signify what had been the signifier, but this new signifier is subject to signification by a still newer signifier, and so on ad infinitum. And each time the tacit operation of the signifier is undermined by being explicitly signified, the functioning of what had been signified by that signifier is also affected. Ultimately then, we have in this “hall of mirrors” neither signifier nor signified in any stable, abidingly meaningful form.
Poststructuralist writing exemplifies the recursive “sliding” or “slippage” of the signifier. The approach of psychoanalyst Jacques Lacan is a prime illustration. For Lacan, language “is constituted by a set of signifiers” that involves what “I call the Other” (1966/1970: 193). The “otherness” of language results from the fact that, in its “chain of signifiers” (194), every act of self-reference, rather than affirming the identity of the self or subject that is referred to, always slips away into what is other, into a new and anonymous signifier. As Lacan puts it:
All that is language is lent from this otherness and this is why the subject is always a fading thing that runs under the chain of signifiers. For the definition of a signifier is that it represents a subject not for another subject but for another signifier. This is the only definition possible of the signifier as different from the sign. The sign is something that represents something for somebody, but the signifier is something that represents a subject for another signifier. The consequence is that the subject disappears….” (1966/1970: 194)
In this way, the sign—which had constituted for earlier semioticians a fixed relationship between a signifier and its signified meaning, with the subject operating stably behind the scenes (the “somebody” to which Lacan alludes)—now dissolves into an evanescent flux of differences wherein the subject loses its substance, becoming a “nobody,” a ghost-like quasi-presence.
Much the same process of dissolution is reflected in the deconstructionist writings of Jacques Derrida. In the “primary writing” (1976: 7) of which he speaks, “[s]ign will always lead to sign, one substituting the other...as signifier and signified in turn” (Spivak 1976: xix). In Derrida’s own words, language must be understood as a field “of freeplay, that is to say, a field of infinite substitutions” (cited by Spivak 1976: xix) in which identity fragments into sheer difference (différance). The specific way this takes place is by the process of self-referential mirroring in which, time and again, the signifier is displaced by being made into what is signified by a newly implicit signifier.
It seems clear that the slippage of the signifier results from the indefinite repetition of recursion. This is the nature of semiosis, we are told; it is a “mirror game” in which self-identity is perpetually subverted and we continually slide into otherness and difference. While I certainly agree with the general consensus among semioticians that symbolic operations are inherently recursive, I propose that the infinite regress to which poststructuralism is prone actually derives from its failure fully to achieve recursion.
Again, when the signifier “slips,” it becomes something that is now itself signified. Yet does this really constitute a concrete instance of self-signification, or does it merely entail the close juxtaposition of two semiotic acts neither of which are recursive in themselves? Initially, X signifies Y. Then there is the reversal of this in which X itself becomes signified by a new signifier, Z. This is obviously not to say that X signifies X. Poststructuralist “self-signification” then does not truly involve a signifier’s reference to itself within the same actual occasion, to use Whitehead’s (1978) term for a fundamental concrete event; it entails only a switching of roles between signifier and signified from one occasion to another. (No doubt occasions may follow each other in close succession and may be broadly construed as belonging to the “same” occurrence; but, on a more concrete level, the occasions of poststructuralism constitute distinct semiotic acts.) Therefore, poststructuralist signification is not radically recursive, not recursive all the way down into the roots of semiosis, for the signifier of occasion 2 does not signify itself but only that which was the signifier on occasion 1.
If poststructuralism fails to meet the challenge of radical self-reference because its signification within the actual occasion is strictly a reference to what is other, does radical recursion involve reference to the self in the sense of simple self-identity (X≡X)? It surely cannot. For without the aspect of the other, of difference, meaning is trivialized and collapses. Radical recursion therefore entails neither external reference nor self-identity. What it constitutes, I suggest, is the dialectical interplay of these.
I propose that, in radical recursion, though the self that is signified is not simply the same self that does the signifying; though the very act of reflecting upon the self turns it into what is other; this other flows right back into the source from which it arises, rather than appearing merely as an other cast before a new self. The semiotic act I am intimating thus would give us neither self nor other, in the categorically opposed sense of these terms. We would realize instead their paradoxical interpenetration. I suggest that this dialectic is what we require to supersede the supremacy of linear signification in a meaningful way. Signifier and signified would be more than reciprocally interdependent in such a self-signification. They would be identical, utterly one. Yet they also would be two. By virtue of the latter aspect, meaningful signification would continue; by virtue of the former, recursion would go all the way down; it would be realized concretely in the heart of the actual occasion. To be sure, this construal of radical recursion requires further explication.
2. RADICAL RECURSION IN TOPOLOGY
Psychoanalyst Jacques Lacan had turned to the science of linguistics in order to clarify the language of the psyche. What we see precisely in the slippage of the signifier through which the subject is “a fading thing” (1966/1970: 194) is the functioning of the unconscious. But Lacan was not content to stop with a merely linguistic clarification of psychic process. In an effort to achieve an even higher level of precision, he appealed to mathematics, and, in particular, to topology, the qualitative sub-discipline that deals with the properties of surfaces. By way of elucidating the signifying activity that constitutes the unconscious discourse of the human subject, Lacan presented a diagram of a Moebius strip:
This diagram can be considered the basis of a sort of essential inscription at the origin, in the knot which constitutes the subject. This goes much further than you may think at first, because you can search for the sort of surface able to receive such inscriptions. You can perhaps see that the sphere, that old symbol for totality, is unsuitable. A torus, a Klein bottle, a cross-cut surface, are able to receive such a cut. And this diversity is very important as it explains many things about the structure of mental disease. If one can symbolize the subject by this fundamental cut, in the same way one can show that a cut on a torus corresponds to the neurotic subject, and on a cross-cut surface to another sort of mental disease. (Lacan 1966/1970: 192–193)
Comparing the sphere and the Moebius strip, we can say that both are recursive, insofar as they both turn back upon themselves. But unlike “that old symbol for totality,” the Moebius possesses a “fundamental cut”; a knot, twist or gap. In Lacan’s view, this cut represents the division inherent in the subject that prevents it from realizing the self-identity symbolized by the sphere. The cut functions like a crack in a mirror, leading the Moebius to signify itself in such a way that it distorts or displaces itself. Or, speaking diachronically, we can say that Moebius recursion is interrupted by the cut and we cut to a new occasion. In moving into the Moebius’s twist, the signifier we started with is twisted into that which is signified by a newly implicit signifier that is a “mirror image” of the original yet out of step with it. On Lacan’s reading then, the Moebius strip embodies the self-alienating kind of recursion that falls short of what I have called radical recursion. I suggest, however, that there is a different way of reading the Moebius. To see how Moebius recursion can be grasped in the radical sense adumbrated above, let us look more closely at this curious topological structure.
We may bring out most effectively the dialectical character of the Moebius strip by comparing it to a non-dialectical structure more similar to it than is the sphere: the cylindrical ring (see Rosen 1994, 2004a).

Figure 1. Cylindrical ring (a) and Moebius strip (b)
A cylindrical ring (Fig. 1a) is constructed by cutting out a narrow strip of paper and joining the ends. The surface of Moebius (Fig. 1b) is produced by giving one end of such a strip a half twist (through an angle of 180°) before linking it with the other. The cylindrical ring possesses the familiar property of two-sidedness: at any point along its surface, two distinct sides can be identified. Commencing on either side, rotation about the ring traces out a circle of simple self-return like that found on the sphere. The two-sidedness of the cylinder of course precludes continuous passage from one side to the other. Such a transition is inevitably cut short at the surface’s edge; the singularity we encounter there tells us that we cannot reach the far side without a break in contact, a cut to a new occasion. We are therefore able to say that, whereas rotation about a single side of the two-sided ring signifies the simply continuous affirmation of self-identity, passage between sides expresses a simply discontinuous cut to what is other.
Now, in the case of the Moebius strip, it is true that if you place your index finger anywhere on the surface, you will be able to put your thumb on a corresponding point on the opposite side. The Moebius strip does have two sides, like the cylinder. But this only holds for the local cross-section of the strip defined by thumb and forefinger. Taking the full length of the strip into account, we discover that points on opposite sides are intimately connected—they can be thought of as twisting or dissolving into each other continuously, as being bound up internally. Accordingly, mathematicians define such pairs of points as single points, and the two sides of the Moebius strip as but one side.
I want to emphasize that the Moebius surface is not one-sided in the homogeneous sense of a single side of the cylindrical ring. It is one-sided in the paradoxical sense, one-sided and also two-sided, for the local distinction between sides is not just negated with expansion to the Moebius as a whole. In coming to interpenetrate each other, the sides do not merely lose their distinct identities. And yet, though the sides remain different, they also become one and the same. Thus, if the cylindrical ring embodies the dualism of identity and difference, of continuity and discontinuity, the Moebius strip signifies their dialectical entwinement. We can say as well that while the cylinder dualistically expresses both trivial recursion (through movement on a single side) and non-recursion (through passage to the other side), the Moebius models radical recursion.
Let us focus on the unique recursive action of the Moebius. With 360° of rotation about this surface, we appear to return to our point of origin. But this return is in fact also a departure, since, instead of remaining on the same side of the strip as in the case of cylindrical rotation, we are carried to the opposite side. So Moebius recursion incorporates an element of discontinuity not evident in its cylindrical counterpart. It is this distinctive feature that Lacan picked up on in contrasting the Moebius with the sphere. What Lacan apparently missed is that the discontinuity of the Moebius, its twist or cut—unlike the cut required in passing from one side of the cylinder to the other—is also continuous. It is in glossing over the paradox of Moebius recursion that Lacan stopped short of radical recursion. Lacan was apparently unable to recognize that the Moebius signifier does not merely short-circuit its reference to itself by prematurely cutting away from itself to an alter-self operative on a new occasion. Rather, the Moebius signification of self as other (and other as self) transpires within the same concrete occasion thereby surpassing the dualism of self and other.
The application of Moebius topology has been taken up by thinkers with diverse orientations and disciplinary backgrounds. From a feminist perspective emphasizing embodiment, theorist Elizabeth Grosz expands on Lacan’s use of the Moebius by portraying it as expressing “the inflection of mind into body and body into mind” (1994: xii). Anthropologist Peter Harries-Jones (2002) suggests that the paradoxical link between culture and environment as understood by Bateson is best depicted in the form of a Moebius strip. Communications philosopher Brian Massumi (carrying forward Deleuze and Guattari’s call for a “topology of multiplicities” [1987: 483]), demonstrates the need to reconceive human transactions via a “strange one-sided topology” that recursively surmounts the old dichotomies by working at a “paradoxically creative edge” (1998). Semiotician Floyd Merrell (1998) uses the paradox of the Moebius to model C. S. Peirce’s concept of abduction. And philosopher Yair Neuman—in this issue of SEED—applies the Moebius to the structure of boundary events in semiotic systems. (My own work with the Moebius dates back to the 1970s; see Rosen 1994.) In these writings, sustained emphasis on paradox allows the authors to surmount Lacanian “slippage” and employ Moebius topology to question effectively “the binary oppositions…[of] mind/body, nature/culture, subject/object and interior/exterior” (Grosz 1994: 164).
It is all too easy, however, to lose one’s paradoxical edge. This is evidenced in Grosz and Massumi when—after using topology to successfully challenge binary opposition on one level of analysis, they appear to fall prey to it on another. Thus, in the case of certain root philosophical oppositions that implicitly structure their thinking—such as the one and the many, identity and difference, being and becoming—they wind up privileging “the fields of difference, the trajectories of becoming” (Grosz 1994: 210). The “one-sidedness” of such a reaction to the totalizing propensities of structuralism (and classico-modernism in general) is certainly not of the Moebius kind. Instead of genuinely questioning the categorial purity of the old approach by consistently applying topological paradox to the most basic philosophical dichotomies, there is a slippage into a sort of “reverse purism” (Rosen, 2004b). Pure identity (totality, unity, being, continuity, etc.) is supplanted by a mode of difference every bit as pure: Derridean différance. It is in the process of unambiguously affirming one member of the philosophical binary over the other that the Moebius edge is lost. So what I am proposing is that the application of topological paradox needs to be implemented in a consistent and thoroughgoing manner all the way down. From my own experience, I know how difficult this is to achieve and it would not surprise me to learn that I myself lose my edge in places in this very text. As a dweller in a “glass house,” I must be careful then about the “stones” I hurl. We are all challenged to avoid limiting our applications of topological paradox to the surface of our discourse while allowing our deepest assumptions and forms of expression to remain tacitly governed by the system of binary logic that has controlled our thinking for so many centuries. To keep our topological edge all the way down and thus achieve radical recursion, we must consistently exceed mere “logics of presence or position” and employ “qualitative topologics,” as Massumi (1998) so well puts it.
3. THE KLEIN BOTTLE
I must now acknowledge a limitation in the Moebius expression of radical recursion. The Moebius does effectively signify the dialectic of continuity and discontinuity. In traversing the twist, we depart from the circle of self-identity associated with continuous rotation about a single side of the cylindrical ring, and we make the transition to the other side of the surface, which, when enacted on the cylinder, brings simple discontinuity. Yet, in the Moebius case, the departure from cylindrical continuity happens continuously. However, the discontinuous aspect of the Moebius dialectic is in fact something of an abstraction. While the effect of discontinuity is surely created in passing through the twist to the far side, there is never any true cut or break, as occurs when actually crossing an edge. The Moebius therefore signifies the continuity-discontinuity dialectic in a continuous way; the discontinuous element is symbolized but not concretely embodied. I suggest that, for a full-fledged realization of the radically recursive dialectic, we require a topological structure in which continuity and discontinuity are interwoven not merely in effect but in actual fact.
There exists a higher-dimensional counterpart of the Moebius surface. By way of introduction, consider an interesting attribute of the Moebius: its asymmetry. Unlike the cylindrical ring, the Moebius has a definite orientation in space; it can be produced either in a left- or right-handed form (depending on the direction in which it is twisted). If both a left- and right-oriented Moebius surface were constructed and then "glued together," superimposed on one another point for point, a Klein bottle would result (Lacan’s passing allusion to this topological structure is cited above).
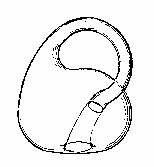
Figure 2.
The Klein bottle
The Klein bottle (Fig. 2) has the same property of asymmetric one-sidedness as the two-dimensional Moebius surface but incorporates an added dimension (Rosen 1994). Note, however, that we cannot actually produce a continuous model of this curious container, for left- and right-facing Moebius bands cannot be superimposed on each other in three-dimensional space without tearing the surfaces. Therefore, while each Moebius enantiomorph is continuous within itself, joining these mirror twins to form a Klein bottle brings discontinuity.
The feature of Kleinian discontinuity can be illustrated by means of a different but mathematically equivalent way of making the bottle. Once again a comparison is called for.
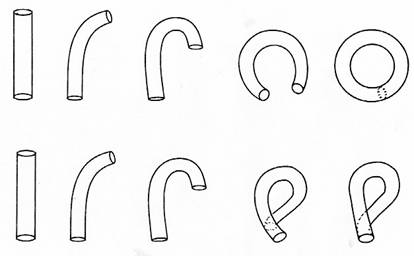
Figure 3. Construction of torus (upper row) and Klein bottle
(lower row)
Both rows of Figure 3 depict the progressive closing of a tubular surface that initially is open. In the upper row, the end circles of the tube are joined in the conventional way, brought together through the three-dimensional space outside the body of the tube to produce a doughnut-shaped form technically known as a torus (a higher-order analogue of the cylindrical ring). By contrast, the end circles in the lower row are superimposed from inside the body of the tube, an operation requiring the tube to pass through itself. This results in the formation of the Klein bottle. Indeed, if the structure so produced were cut in half, the halves would be Moebius bands of opposite handedness. But in three-dimensional space, no structure can penetrate itself without cutting a hole in its surface. So, from a second standpoint, we see that the continuous construction of a Klein bottle cannot be carried out in the three dimensions available to us. The Klein bottle thus seems to possess the element of concrete discontinuity missing from its lower-dimensional Moebius counterpart. Whereas the twist in the Moebius mediates the transition from one side of the surface to the other in a continuous fashion, the Kleinian passage from inside to outside requires a hole. Of course, a simply discontinuous structure will serve us no better than a simply continuous one if we are seeking to express the dialectic of continuity and discontinuity. What is needed is a structure that embodies the paradoxical interweaving of continuity and discontinuity. And, in fact, the Klein bottle does just that, provided that we approach it in a truly dialectical way.
How does modernist mathematics approach the Klein bottle? Mathematicians certainly do not just accept the discontinuity of the Klein bottle. Instead they rely on the idea that a form that penetrates itself in a given number of dimensions can be produced without cutting a hole by invoking an added dimension. The point is nicely illustrated by the mathematician Rudolph Rucker (1977). He asks us to imagine a species of "flatlanders" attempting to assemble a Moebius strip. Rucker shows that, since the space inhabited by these creatures would be limited to two dimensions, when they would try to make an actual model of the Moebius, they would be forced to cut a hole in it. Of course, no such problem arises for us human beings, who have full access to three dimensions. It is the continuous construction of the Klein bottle that seems problematic for us, since this would appear to require a fourth dimension, but, try as we might, we find no fourth dimension in which to execute the operation. For modernist mathematics, however, there is actually no problem. Although dimensions higher than the third may be unavailable to concrete experience, mathematicians feel free to proceed abstractly, calling forth as many extra dimensions as they wish. Added dimensions are summoned into being by extrapolation from the known three-dimensionality of the physical world. This theoretical procedure of dimensional proliferation presupposes that the nature of dimensionality itself is left unchanged. In the case of the Klein bottle, the "fourth dimension" required to complete its formation remains an extensive continuum as is three-dimensional space, though the "higher” space is taken as "imaginary"; the Klein bottle, for its part, is regarded as an "imaginary object" embedded in this space. Enclosed as it is in the hypothesized four-dimensional continuum, the imaginary Klein bottle itself is presumed simply continuous. Like the Moebius strip of three-dimensional space, it is thought to possess nary a hole.
Now, in his phenomenological study of topology, the mathematician Stephen Barr advised that we should not be intimidated by the “higher mathematician....We must not be put off because he is interested only in the higher abstractions: we have an equal right to be interested in the tangible” (1964: 20). The tangible fact about the Klein bottle that is glossed over in the higher abstractions of modernist mathematics is its hole. Because the standard approach has always presupposed extensive continuity, it cannot come to terms with the inherent discontinuity of the Klein bottle created by its self-intersection. Therefore, all too quickly, “higher” mathematics circumvents this hole by an act of abstraction in which the Klein bottle is treated as a closed object embedded in a hyper-dimensional continuum. To be sure, an “added dimension” is needed if the Klein bottle is not to be regarded as merely discontinuous. When limited to the three dimensions of ordinary space, the Klein bottle cannot give expression to the dialectic of continuity and discontinuity. But the “added dimension,” rather than being a continuum, must itself blend continuity and discontinuity.
In a continuum, all interactions occur between fixed terms that are externally related. The point elements of which the continuum is composed are themselves related in this manner. As philosopher Milič Čapek put it in his reflection on classical space, “no matter how minute a spatial interval may be, it must always be an interval separating two points, each of which is external to the other” (1961: 19). In the words of Martin Heidegger, the continuum is essentially constituted by the “‘outside-of-one-another’ of the multiplicity of points” (1927/1962: 481). Given the fundamental exteriority of classical space, relations among objects and events contained within it must also be external. In the continuum, systems “interact through forces that do not bring about any changes in their essential natures…[they interact] only through some kind of external contact” (Bohm 1980: 173). Generally speaking then, the notion of the continuum implies that all boundaries are external in nature. This includes the point elements that bound space; the boundaries between and among interacting objects, systems, and events in space; and the figure-ground boundary that distinguishes an entity from its spatial context.
One other kind of exterior boundary is implicit in the classico-modernist approach: the one that separates the object being observed from the subject that observes or analyzes it. Whereas objects are embedded in the extensive continuum, the subject entails discontinuity. In the language of Descartes, the object is res extensa and the subject res cogitans, thus unextended, not manifested in space. However, this distinction is complicated by the subtlety of the continuum idea. The continuum actually possesses its own aspect of discontinuity. Even though the points composing space are packed densely together, because these points are related to one another externally, the continuum is infinitely divisible; it can be indefinitely partitioned into ever smaller segments (the mathematician Charles Muses was thus prompted to describe the continuum as actually constituting an “infinite discontinuum” [1968: 37]). It naturally follows that the objects embedded in this medium are themselves partible; they can be rendered discontinuous. The discontinuity associated with the subject, on the other hand, signifies its transcendence of the continuum. So, whereas the breach one may produce in an object in fact reflects a property of the continuum, the subject constitutes a break with that continuum. Although it may rightly be said that classico-modernism favors continuity over discontinuity, what we are seeing is that there is indeed a place for discontinuity in the conventional paradigm, albeit a tacit or negative one. At the deepest level, it is the division of continuity and discontinuity that classico-modernism upholds.
4. RADICAL RECURSION AND THE DIMENSION OF DEPTH
The classical concept of dimension has prevailed from the time of Descartes and Kant to the physics and mathematics of today. In mainstream science and philosophy, the exteriority of relations among objects in space, and between object and subject, has not been questioned in a fundamental way. Yet countercurrents do exist. We find evidence of these in the works of process-oriented thinkers such as Heidegger (1962/1972), Gendlin and Lemke (1983), and Bateson (see Neuman’s topological interpretation of Bateson in this issue of SEED, and Harries-Jones’s [1995] account of Bateson’s recursive vision); in each case, internal dynamics are given precedence over the static externality of the spatial continuum (see also Rosen 1994, 2004a). One of the most explicit formulations of process dimensionality is found in the notion of depth advanced by the phenomenological philosopher Maurice Merleau-Ponty (1964). This idea provides us with an insight into dimension that permits us to surpass the limits of classico-modernism and arrive at a radically recursive understanding of space that is well suited for expressing the Kleinian dialectic of continuity and discontinuity.
By way of introducing Merleau-Ponty’s depth dimension, let us consider in greater detail the traditional dichotomy between the objects contained in space and their spatial container, or, as Plato put it, between “that which becomes [and] that in which it becomes” (1965: 69). A visible form “becomes,” whereas that “in which it becomes” is “invisible and formless” (1965: 70). Whatever changes may transpire in the objects that “become,” however they may be transformed, the containing space itself does not change. Indeed, for there to be change, there must be difference, contrast, dialectical opposition of some kind. But the point-elements that make up the classical continuum, rather than entailing opposition, involve mere juxtaposition. Unextended and thus devoid of inner structure, the elements of space possess no gradations of depth; no shading, texture, or nuance; no contrasts or distinctions of any sort. Instead of expressing the dialectical interplay of shadow and light, space itself is all light, as it were. A condition of “total exposure” prevails for the point-elements of the continuum, since these elements, having no interior recesses, must be said to exist solely “on the outside.” All that can be said of the relations among such eviscerated beings is what Heidegger said: the points of classical space are “‘outside-of-one-another’” (1927/1962: 481). So, rather than actively engaging each other as the beings that are contained in space seem to do, the densely packed elements of the classical container sit inertly side by side, like identical beads on a string.
In fact, even though the beings that dwell in such a space can be described as “actively engaged,” we have seen that the quality of their interaction is affected by the context in which they are embedded: since the continuum is constituted by sheer externality, the relations among its inhabitants must also be external. Classical dynamics are essentially mechanistic; instead of involving a full-fledged dialectic of opposition and identity wherein beings influence each other from core to core, influence is exerted in a more superficial fashion, “only through some kind of external contact” (Bohm 1980: 173). We may say then that classical space contains dialectical process in such a way that it externalizes it, divesting it of its depth and vitality.
It is the classico-modernist view of space that Merleau-Ponty calls into question. What he demonstrates is that the spatial continuum appearing to contain dialectical process actually originates from it.
In his essay “Eye and Mind,” Merleau-Ponty emphasizes the “absolute positivity” of traditional Cartesian space (1964: 173). For Descartes, space simply is there; possessing no folds or nuances, it is the utterly explicit openness, the sheer positive extension that constitutes the field of strictly external relations wherein unambiguous measurements can be made. Merleau-Ponty speaks of
this space without hiding places which in each of its points is only what it is....Space is in-itself; rather, it is the in-itself par excellence. Its definition is to be in itself. Every point of space is and is thought to be right where it is—one here, another there; space is the evidence of the “where.” Orientation, polarity, envelopment are, in space, derived phenomena inextricably bound to my presence [thus “merely subjective”]. Space remains absolutely in itself, everywhere equal to itself, homogeneous; its dimensions, for example, are interchangeable. (1964: 173)
Merleau-Ponty concludes that, for Descartes, space is a purely “positive being, outside all points of view, beyond all latency and all depth, having no true thickness” (1964: 174).
Challenging the Cartesian view, Merleau-Ponty insists that the dialectical features of perceptual experience (“[o]rientation, polarity, [and] envelopment”) are not merely secondary to a space that itself is devoid of such features. He begins his own account of spatiality by exploring the paradoxical interplay of the visible and invisible, of identity and difference, that is characteristic of true depth:
The enigma consists in the fact that I see things, each one in its place, precisely because they eclipse one another, and that they are rivals before my sight precisely because each one is in its own place. Their exteriority is known in their envelopment and their mutual dependence in their autonomy. Once depth is understood in this way, we can no longer call it a third dimension. In the first place, if it were a dimension, it would be the first one; there are forms and definite planes only if it is stipulated how far from me their different parts are. But a first dimension that contains all the others is no longer a dimension, at least in the ordinary sense of a certain relationship according to which we make measurements. Depth thus understood is, rather, the experience of the reversibility of dimensions, of a global “locality”—everything in the same place at the same time, a locality from which height, width, and depth [the classical dimensions] are abstracted. (1964: 180)
Speaking in the same vein, Merleau-Ponty characterizes depth as “a single dimensionality, a polymorphous Being,” from which the Cartesian dimensions of linear extension derive, and “which justifies all [Cartesian dimensions] without being fully expressed by any” (1964: 174). The dimension of depth is “both natal space and matrix of every other existing space” (1964: 176).
Merleau-Ponty goes on to observe that primal dimensionality must be understood as self-containing. This is illustrated through a discussion of contemporary art, and, in particular, the work of Paul Cézanne: “Cézanne knows already what cubism will repeat: that the external form, the envelope, is secondary and derived, that it is not that which causes a thing to take form, that this shell of space must be shattered, this fruit bowl broken” (1964: 180). In breaking the “shell,” one disrupts the classical representation of objects in space. Merleau-Ponty asks:
[W]hat is there to paint, then? Cubes, spheres, and cones...? Pure forms which have the solidity of what could be defined by an internal law of construction...? Cézanne made an experiment of this kind in his middle period. He opted for the solid, for space—and came to find that inside this space, a box or container too large for them, the things began to move, color against color; they began to modulate in instability. Thus we must seek space and its content as together. (1964: 180)
The work of Cézanne is Merleau-Ponty’s primary example of the exploration of depth as originary dimension. The foregoing passage describes Cézanne’s discovery that primal dimensionality is not space taken in abstraction from its content, but is the unbroken flow from container to content. It is in this sense of the internal mediation of container and content that Cézanne’s depth dimension is self-containing.
Merleau-Ponty also makes it clear that the primal dimension engages embodied subjectivity: the dimension of depth “goes toward things from, as starting point, this body to which I myself am fastened” (1964: 173). In commenting that, “there are forms and definite planes only if it is stipulated how far from me their different parts are” (180; italics mine), Merleau-Ponty is conveying the same idea. A little later, Merleau-Ponty goes further:
The painter’s vision is not a view upon the outside, a merely “physical-optical” relation with the world. The world no longer stands before him through representation; rather, it is the painter to whom the things of the world give birth by a sort of concentration or coming-to-itself of the visible. Ultimately the painting relates to nothing at all among experienced things unless it is first of all “autofigurative.”....The spectacle is first of all a spectacle of itself before it is a spectacle of something outside of it. (1964: 181)
In this passage, the painting of which Merleau-Ponty speaks, in drawing upon the originary dimension of depth, recursively draws in upon itself. Painting of this kind is not merely a signification of what is other, but a concrete self-signification that undercuts the external boundary between signifier and signified.
In sum, the phenomenological dimension of depth as described by Merleau-Ponty is (1) the “first” dimension, inasmuch as it is the source of the Cartesian dimensions, which are idealizations of it; it is (2) a self-containing dimension, not merely a container for contents that are taken as separate from it; and it is (3) a dimension that blends subject and object concretely, rather than serving as a static staging platform for the objectifications of a detached subject. In realizing depth, we surpass the concept of space as but an inert container and come to understand it as an aspect of an indivisible cycle of action in which container, contained, and “uncontained”—space, object, and subject—are integrally incorporated.
The work of Merleau-Ponty provides us with an insight into the nature of the “added dimension” that is required for the Kleinian signification of radical recursion. It would not be enough to say that the Klein bottle makes use of the dimension of depth to realize its dialectic of continuity and discontinuity—not if “makes use” connotes the operation of a model employing a containing medium to signify a meaning external to itself. It is perhaps more accurate to say that the Klein bottle is the depth dimension. For, rather than being a model contained as object-in-space, the Klein bottle—grasped in terms of depth—is the inseparability of object, space, and subject, the unbroken circulation of these intimated by Merleau-Ponty.
It is the unique hole in the Klein bottle that plays the pivotal role. This loss in continuity is necessary. One certainly could make a hole in the torus, or in any other object in three-dimensional space, but such discontinuities would not be necessary inasmuch as these objects could be fully assembled in space without rupturing them. It is clear that whether an object like the torus is cut open or left intact, the closure of the space containing that object will not be brought into question; in rendering such an object discontinuous, we do not affect the assumption that the space in which it is embedded is a continuum. Indeed, we have seen that the divisibility of an ordinary object derives from the infinite divisibility of the continuum itself. With the Klein bottle it is different. Its discontinuity does challenge the continuity of three-dimensional space as such, for the necessity of the hole in the bottle indicates that space is unable to contain the bottle the way ordinary objects appear containable. We know that for the Kleinian “object” to be brought to completion, assembled without a hole, an “added dimension” is required, and I am proposing that the dimension to be engaged is that of Merleau-Pontean depth (assuming we do not wish merely to skip over the hole by a continuity-maintaining act of abstraction, as in the standard mathematical stratagem for dealing with the Klein bottle).
In the depth dimension, while the hole in the Klein bottle is no mere breach in an object in space, neither is it simply a rupture in space per se that corresponds to the subject. Rather, the Kleinian “hole” is in fact a dialectical (w)hole resulting from an act of self-intersection wherein the purported object does the “impossible”: it passes unbrokenly through itself, and, in so doing, flows backward into its own subjective ground (in Merleau-Ponty’s terms, it is “autofigurative”). Elsewhere, I noted the resemblance of the Klein bottle to the hermetic vessel of old alchemy (Rosen 1995). The design of the enigmatic vessel is essentially that of the uroboros, the serpent that consumes itself by swallowing its own tail. To contain itself, the serpent must intersect itself, an operation requiring a hole (corresponding to the opening that is its mouth). The hole in the Klein bottle is of this sort. It is neither solely a hole in a container, nor a hole in that which it contains, but the hole produced by the recursive act of self-containment that integrates the container with its contents in this way giving (w)holeness.
The Kleinian process of self-containment enacted through the dimension of depth is surely no trivial recursion, no regression of meaning to simple self-identity. The Klein bottle refers to itself, but it also makes reference to what is other and a boundary is crossed. Of course, the boundary in question is not of the exterior sort so familiar to us; instead it is paradoxical, a boundary that is not a boundary (see Neuman, this issue of SEED, and Rosen 1997, 2004a). In passing through Kleinian depths from self to other (subject to object, the discontinuous to the continuum), we cross over the boundary to the “far side,” yet at once remain on the “near side.” In this way, while the self-other distinction is not just abrogated, the supremacy of this distinction is overcome and we realize a harmony of self and other so intimate that the prior meanings of these terms are transmuted. The erstwhile categorical purity of self and other is supplanted by an odd uroboric hybrid, a “hermaphroditic” fusion wherein self and other, though assuredly different, are one and the same. This profoundly paradoxical manner of self-reference is what I mean by radical recursion.
5. SEMIOTIC POSTSCRIPT
The subtlety of the notion of radical recursion has not been exhausted by what I have written above. I will note another layer of meaning before I conclude.
Consider the words “Klein bottle.” Although these signifiers point to the depth-dimensional structure that embodies the paradox of radical self-signification, the signifiers themselves—“K-l-e-i-n” and “b-o-t-t-l-e”—are but arbitrarily devised, conventionally agreed upon tokens that refer to their content in a merely external manner. These one-dimensional typographic marks appearing on the two-dimensional surface of this page obviously fall short of tangibly delivering the three-dimensional Kleinian depth they signify. To the extent that “unmotivated” conventional marks constitute the primary mode of signification for this text, the old division between signifier and signified will be upheld and the meaning of the Klein bottle will remain an abstraction.
In seeking to close the gap between signifier and signified, it might be feasible to place greater emphasis on our two-dimensional images of the Klein bottle (Figs. 2 and 3), or, better still, to work with a full three-dimensional model of this paradoxical structure (a model can be constructed with a flexible length of tubing such as that illustrated in Fig. 3). However, it should be clear by now that for the Klein bottle to be fully dimensioned, our model cannot be limited to an object in three-dimensional space. The Klein bottle must be realized in Merleau-Pontian depth. To this end, rather than regarding the Klein bottle as but an object appearing before us, something “out there” in space that we see and can handle, we must resist this compulsion of naïve realism and take the bottle as something that we read. What I am suggesting is that, while the Klein bottle cannot be actualized in the abstract universal medium of words alone, neither can it be brought to fruition as but a particular concrete thing; to be realized in depth, it must be realized as a hybrid of word and thing (a “general thing”; Merleau-Ponty 1968: 139), as a “tangible word” or iconic text. In the capacity of iconic sign, the Klein bottle can serve to “motivate” the process of signification by raising it from one-dimensional arbitrariness to a fully committed three-dimensional intercourse of signifier and signified.
In reading our iconic Kleinian text, we must of course read its hole. Instead of interpreting the hole as a gap in an ordinary object contained in space, we are to read it as an opening to a “higher dimension,” and read that dimension “autofiguratively,” grasping it as the prereflective source of our very own reading. The hole then becomes a (w)hole that we actualize in depth as we pass unbrokenly from text back to subtext in a uroboric act of radical recursion. Here the Klein bottle signifies radical recursion by signifying itself. Or in Peircian terms, we may say with semiotician Paul Ryan that the Klein bottle is a “sign of itself” (1993: 345–347).
REFERENCES
Barr, Stephen. 1964. Experiments
in Topology.
Bohm, David. 1980. Wholeness and
the Implicate Order.
Čapek, Milič. 1961. Philosophical
Impact of Contemporary Physics.
Deleuze, Gilles, and Felix Guattari. 1987. A Thousand Plateaus:
Capitalism and Schizophrenia.
Derrida,
Jacques. 1976. Of
Grammatology. Trans. Gayatri C. Spivak.
Gendlin, Eugene T., and Jay L. Lemke. 1983. A Critique of Relativity and Localization. International Journal of Mathematical Modelling, 4: 61–72.
Grosz, Elizabeth. 1994. Volatile
Bodies.
Harries-Jones, Peter. 1995. A Recursive Vision: Ecological Understanding
and Gregory Bateson.
———. 2002. Where Bonds Become Binds: The Necessity for Bateson’s Interactive Perspective on Biosemiotics. Sign Systems Studies, 30 (1): 163–181.
Heidegger, Martin. 1927/1962. Being and Time. Trans. J. Macquarrie and E. Robinson.
———.
1962/1972.
Time and Being, in J. Stambaugh, trans., On Time
and Being, pp. 1–24.
Lacan, Jacques. 1966/1970. Of Structure as an Inmixing
of an Otherness Prerequisite to Any Subject Whatever, in R. Macksey
and E. Donato, eds., The Languages of Criticism and the Sciences of Man: The Structuralist
Controversy, pp. 186–200.
Massumi, Brian. 1998. Strange Horizon: Buildings, Biograms, and the Body Topologic. Retrieved February 15, 2003, from Indiana University Web Site: http://www.indiana.edu/~thinkmat/strange.doc.
Merleau-Ponty, Maurice. 1964. Eye and Mind, in J. M. Edie,
ed., The Primacy of Perception, pp. 159–190.
———.
1968. The Visible
and the Invisible.
Merrell, Floyd. 1998. Simplicity and Complexity.
Muses, Charles. 1968. Hypernumber and Metadimension Theory. Journal of Consciousness Studies, 1: 29–48.
Neuman, Yair. 2003. Moebius and Paradox: On the Abstract Structure of Boundary Events in Semiotic Systems. SEED Journal, this issue.
Plato. 1965. Timaeus and Critias. Trans. D. Lee.
Rosen,
Steven M. 1994. Science, Paradox, and the Moebius Principle.
———.
1995. Pouring Old Wine into a New Bottle, in M. Stein,
ed., The Interactive Field in Analysis, pp. 121–141.
———. 1997. Wholeness as the Body of Paradox. Journal of Mind and Behavior, 18 (4): 391–424.
———.
2004a. Dimensions of Apeiron: A Topological Phenomenology of Space, Time,
and Individuation.
———. 2004b. Topologies of the Flesh: A Multidimensional Exploration of the Lifeworld. Unpublished manuscript.
Rucker, Rudolph. 1977. Geometry, Relativity, and the Fourth Dimension.
Ryan, Paul. 1993. Video Mind/Earth Mind: Art, Communications,
and Ecology.
Spivak, Gayatri C. 1976. Translator’s
Preface, in J. Derrida, Of Grammatology, pp. ix-lxxxvii.
Whitehead, Alfred North. 1978. Process
and Reality.