Autocreative Hierarchy I:
Structure – Ecosystemic Dependence and Autonomy
Ron Cottam, Willy Ranson and Roger Vounckx
The Evolutionary Processing Group
IMEC Brussels, ETRO
Brussels Free University (VUB)
Pleinlaan 2, 1050 Brussels, Belgium
evol@etro.vub.ac.be
©This paper is not for reproduction without permission of the authors.
ABSTRACT
The natural sciences experience great difficulty in addressing the nature of life. Most particularly, self-consistent theories of observable scalar differences across biological systems are lacking. We have developed a rational scheme for modeling the natural emergence of multi-level hierarchies, and for the characterization of hierarchical entities and systems. This paper describes the resultant birational structure which may be attributed to a real hierarchy. The emergence of new levels is related to the cross-scale transport of both order and novelty, and hierarchical development is attributed to inter-level negotiation of dependence and autonomy. Hyperscalar precursors of understanding and learning, and of complementary logical and emotional operations appear naturally in hierarchies as a consequence of their global stabilization.
1. INTRODUCTION
It is difficult to see how any large unified system could exist or operate successfully without recourse to hierarchy. But this conclusion is very much a case of putting the cart before the horse, as its validity rests on an extensive set of presuppositions and conditional judgments. We will attempt in this paper to sketch out the network of ideas supportive of the proposition, without falling foul of the many and varied philosophical and other pitfalls with which the landscape is littered. We will mainly restrict ourselves in the present instance to the examination of structural aspects of Hierarchy, Ecosystemic Dependence and Autonomy, and leave most of the discussion of contributive and consequent dynamical aspects to a further paper (“Autocreative Hierarchy II: Dynamics – Self-organization, Emergence and Level-changing”).
A necessary starting point is the definition of our subject matter: what do we mean by a large unified system? Unfortunately, this expression does not readily lend itself to reductive linguistic processing, as the elements of the complete expression are inter-dependent: we cannot establish definitions of the words large, unified and system in isolation and then extract the complete expression’s meaning by simply combining them. However, this apparent failure is precisely the definition we require for the expression; or rather it provides a simplified representation of it. Two aspects are important here. The first is that a large unified system can only exist as a partial negation of, or ambiguity in, its own state; the second is that we must in some way match this partiality with the descriptive forms we adopt. An example of the (ontological) former is that a localized entity in a global environment must not only be isolated from it but must also communicate with it (Cottam, Ranson and Vounckx 1999a); an example of the (epistemological) latter is the inability of precise mathematics to describe quantum interactions (except by formulating a precisely defined probabilistic version of a dynamically uncertain event!)[i].
The style of system to which we will refer is one which consists of a large number of partially autonomous[ii] entities whose interactions define the character of the system. This, although seemingly reasonable, is again a self-referential mess on our route to hierarchy! We will restrict ourselves to pointing out part of this problem, and (necessarily) leave the rest to the reader’s interpretive powers. For a group of (partially-) autonomous entities to “be” or “create” a “unified” system, they must communicate. However, communication speed is (conventionally) considered to be restricted (to the speed of light). Consequently, as the number of entities is increased, the definition of systemic character and systemic unity becomes subservient to requirements for reaction to internal or external stimuli. Beyond a certain size and/or complication a system will become noticeably less able to react to stimuli within a suitable time scale and will appear sluggish or un-reactive. If the stimuli are critical it may (will) disintegrate[iii]. This difficulty not only applies to natural or “real” systems, but also to more abstractly-constrained ones, such as digital computers: as a digital processor system is expanded it becomes more and more difficult to maintain formal coherence across the complete array of binary gates, and the gate set-up time as defined by the clock speed must be increased, resulting in a reduced processing rate.
Biological systems have followed a different route in solving this problem. As a biosystem’s size increases beyond critical limits it breaks down into smaller more locally-autonomous regions, whose new larger-scale interactions approximate those which would otherwise exist between smaller-scale entities within the different regions[iv]. This permits the system to react rapidly and effectively to large scale stimuli without taking concurrent account of temporal restrictions at lower levels of organization. Our own brains exhibit an important example of this temporal response-switching through fear-learning (LeDoux 1992) where a subsidiary reactive pathway (via the amygdala) short-circuits the normal cortex response in possibly threatening situations. Hierarchical development is arguably the precursor for higher-level symbolic representation in biosystems, and its copying, through symbolic representation, provides the basis for all of the complicated “machines” which our species has developed.
In the body of this paper, our “sketch” of the network of ideas behind the universality of hierarchical structure will of necessity be just that: a sketch! For other aspects and more complete descriptions we refer the reader to further papers by the present authors, and to extensive work by Stan Salthe, Koichiro Matsuno, Edwina Taborsky, John Collier and Jay Lemke, amongst others.
2. BALLS, STICKS, BODY AND MIND
We will begin by looking at the ubiquitous problem of “viewpoint”. We often describe a system’s informational pathways and their meeting points by the simple picture of a network of “balls and sticks”. The balls represent not only entities, but also communicational nodes; the sticks represent communicational pathways. We must decide very clearly where we are looking things from, as we only have one point of view at one point in time. A system can be described from an external platform, where accessible characteristics are purely global ones. It can also be described from a quasi-external platform as a set of internal relations. This latter corresponds to just about every system analysis which we carry out, but unfortunately in a system which exhibits scale effects internal detail is incompletely accessible through the application of formal rationality (Cottam, Ranson and Vounckx 1999a). On the simplifying presupposition that nearby viewing platforms will most resemble the one we are currently standing on, we will try and approach this problem by distinguishing between directly and indirectly accessible inter-elemental system connections. Direct relationships are established by inter-elemental negotiation of both rationality and context directly and intimately between the elements concerned, as shown in Figure 1. Indirect relationships between elements are those which of necessity pass through other intermediate elements, which are then to some extent free to impose their own modifications on forwarded information.
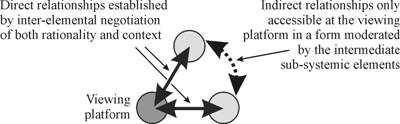
Figure 1. Direct and indirect relationships for a 3-body system with a chosen viewing platform.
We can extend this distinction of direct and indirect linkages to larger ball-and-stick system models. We address as an example the simplest multi-nodal system network form where each node is singly-connected to all the others. Given 3 elements there will be 2 direct links and 1 indirect; with 4 elements, 3 direct, 3 indirect; with 5 elements, 4 direct, 6 indirect, and so on. As we move to larger systems the relationship between direct and indirect links takes on a clear form: the number of direct links goes up as the number of elements (N), the number of indirect links goes up as the square of the number of elements N2/2, as shown in Figure 2: the populations of direct and indirect character co-evolve at very different rates. For a scalar-network system with one million direct links, there are a possible million-million indirect ones: for large systems indirect links are likely to dominate massively, depending on the complexity of the relationship between local and global structures[v]. The character we can attribute to a complete system is ultimately controlled by this direct/indirect balance.
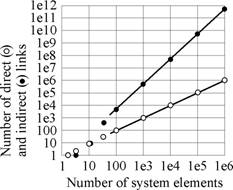
Figure 2. The growth of direct and indirect links in a large multi-element scalar network.
The co-evolution of direct and indirect relations in large systems leads ultimately to two different quasi-independent systemic characters. One corresponds to the "normally scientific" view, which depends on formally-rational cross-scale information transport, the other to parts of the holistic system which are inaccessible to a "normally scientific" viewpoint, and which are associated with the (formally!) distributed nature of indirect relations. Complete representation of systemic interactions with an environment requires evaluation of both of these characters. If we simply describe a quasi-externally viewed system in terms of the reductively specified interactions we risk missing out the majority of the systemic character! (except if we are dealing with “time-independent” artificial formal "machines", such as idealized digital computer systems).
We believe that the bifurcation of systemic character into dual reductive and holistically-related parts and the difference in reductively-rational accessibility between these two characters has led to the conventional split between body and mind, where the body is naturally associated with direct "scientific" bio-systemic relations and the "mind" is naturally "difficult" to understand in the context of a "normally scientific" viewpoint which presupposes that all essential systemic aspects can be related to a single localized platform.
3. MULTI-LEVEL SYSTEMS AND UPSCALING
As soon as we (externally) describe a system as having internal processes, we have attributed to it a degree of hierarchality. Stan Salthe (1993) would maintain that a hierarchical system must have at least three recognizable levels: in this example, we ourselves provide the third level, in our role as observers. Natural hierarchies develop by the “emergence” of higher-level system representations, through reduction in the descriptive informational content. “Fish”, for example, can be viewed as a quasi-symbolic informationally-reduced representation of a lower-level set of characteristics, which could be “body, head, tail, teeth”, whose content is unfortunately insufficient to enable us to avoid sharks and piranhas (or, indeed, for them to be aware that they can eat us!).[vi]
As a simplistic pictorial aid, we adopt the scheme of a “model hierarchy” as shown in Figure 3 to display a hierarchical set of models and their relationships. Possibly-numerous hierarchical levels of a single entity are presented in terms of their perceptual scale (Langloh, Cottam, Vounckx and Cornelis 1993; Cottam, Ranson and Vounckx 2000b) from many-small-scale-components at the left to fewer-large-scale-components at the right, and the vertical line-lengths indicate the superficial informational content of each model. It should be noted that this scheme is far more complicated than it seems, as not only can the different models co-exist (e.g. a tree as cells, a tree as branches, a tree “itself”), but higher-level ones (towards the right hand side) implicitly “include” those towards the left. Of necessity, adjacent models are separated by complex regions (Cottam, Ranson and Vounckx 1998b) which take account of the less-than-formal nature of transitions between representations of different order.
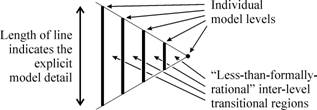
Figure 3. Representing a model hierarchy, from complicated representations (towards the left of the figure) to the simplest binary representation (on the right).
Stan Salthe describes two different classes of hierarchy, namely the “scalar” hierarchy and the “specification” hierarchy (Salthe 1985). He points out that “hierarchies are just models, after all!” (Salthe 2001), and that in his sense our construction is “functionally a specification hierarchy, of levels that happen to be constructed over scale” (idem). We believe, however, not only that natural entities can only be perpetuated in hierarchically-related forms, but that all “real” hierarchies fall into the class we describe, as they are all without exception based on bandwidth-limited (i.e. scaled) real-sensor perception or (more to the point) self-perception, and not on any externalist-defined absolutist constraint (Cottam, Ranson and Vounckx 2000b). It is clear that the only advantage in describing as “hierarchical” an artificially created system which exhibits formally-rational transitions between scales is that it may (but not necessarily) make it easier to “understand” how the system works. Without the imposition of external constraints, such a structure would immediately collapse to a single level.
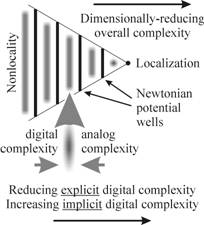
Figure 4. A generalised complementary hierarchical system.
Figure 4 illustrates the further development of this perceptually-scaled hierarchy. Individual model levels constitute Newtonian potential wells in an otherwise complex universal phase space which changes from nonlocality at the left of the figure to extreme localization at the right hand side (Cottam, Ranson and Vounckx 1997), positioned in such a manner that local Newtonian characteristics correspond closely to more global ones.
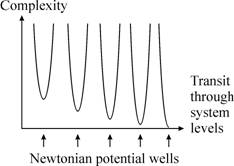
Figure 5. Newtonian potential wells through a naturally-developed hierarchical structure, showing locally reduced well complexity in an otherwise highly complex phase space.
Figure 5 illustrates a “cross-section” of the structure, where the vertical axis indicates the complexity of local representation: the Newtonian wells correspond to those regions of the phase space for which simple causal relations can be drawn for inter-entity processes. This makes it possible for local processes to take place without time-consuming recourse to system globality, and without fear of the appearance of local-global contradiction at some future time. Transit between levels involves sequential passage through two different complex regions, one related to analog approximation and the other to digital approximation (Cottam, Ranson and Vounckx 2001a).
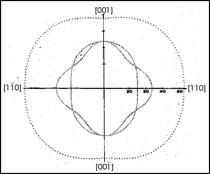
Figure 6. The elastic profile of GaAs in a (110)-type plane.
Across the entire structure there is a balance between the information content of the local explicit representation of the entity and its local implicit information content: simpler descriptions hide more information than complicated ones. Unfortunately, however, information appears to be lost on moving towards the right hand side from local representation to (simpler) local representation, which makes it (apparently) impossible for a level to communicate with other levels which are more towards its left (in the manner that a Boolean AND gate is irreversible in its operation). Perfect cross-scale information transport will cause a hierarchy to collapse, but in the absence of cross-scale transport the hierarchy ceases to exist. This results in the stabilizing compromise of "autonomy negotiation", with the development of partial en-closure of hierarchy levels, partial cross-enclosure transport, and the establishment of inter-level "complex" regions.
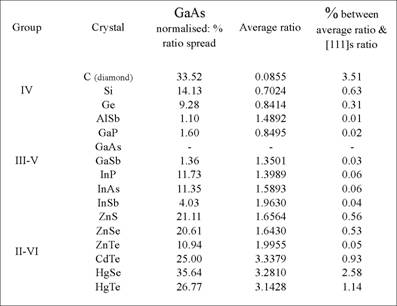
Figure 7. Comparison between the elastic profile of GaAs and those of other zinc-blende crystals. Percentages in the last column indicate the profiles’ differences from that of GaAs.
Most specifically, it is the overall or reduced information transport between the local and the global which concerns us in this instance, and especially upscale or local-to-global information transport, if we wish to address the generation of "high-level" “complex” systems from an assembly of “lower-level” elements. While most usually it is the novelty of appearances at a higher level which attracts attention, the vast majority of cross-scale transported information in a hierarchical system corresponds to order and not novelty.
This is most clearly the case for classical crystals, where the bias is very strongly towards upscale transmission of order, although a degree of other information is involved. These effects can be observed practically in the transmission of ultrasonic waves through single crystals. Figure 6 shows orientational-dependence of the speed of sound in a (110)-type plane of a single GaAs crystal.
Figure 7 lists the differences in the (110) plane between the {shear elasticity spread} and the {average shear elasticity} for the IV, III-V and II-VI zinc-blende crystals, normalized to the values measured for Gallium Arsenide. Materials close in nature to GaAs show marginal differences: the elasticity profile is effectively determined by the lattice structure. Far from GaAs a contribution appears which is dependent on the types of atom present in the lattice. For these zinc-blende materials, at least, the majority of the cross-scale transport is of structural order associated with the crystal lattice, but there is also a small additional part which is associated with the types of atoms which are present.
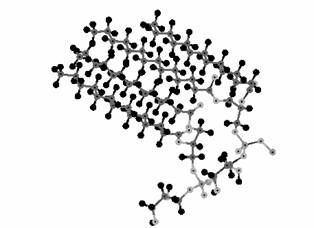
Figure 8: The “partially” crystalline appearance of lipid pdmpg.
The most immediately interesting cross-scale information transport in biological systems is similarly upwards from the microscopic to the macroscopic. In biological systems, reproduction of an organism is controlled by information which is transported upwards in scale, from amino acids, to DNA, to cells, ... . This resembles the upscaling of crystal features we referred to above. Structural regularity at one level acts as a "carrier" for less regular, more specific information, from that scale up to the next. Examination of the shapes of bio-molecules reveals a preponderance of regular structures based on carbon chains and rings, notably the amino acids, photosynthetics, lipids (most especially pdmpg: see Figure 8), and ultimately DNA itself. In a manner somewhat reminiscent of Erwin Schrödinger's propositions in his book "What is Life?" DNA exhibits a "partially crystalline" nature. Regularity is evident at all its different scales, and at its lowest level the 4-base-pair coding provides a "distributed" unit cell.
It is usual to categorize bio-molecules on the basis of their locations and structures in sequence space. Examination of sequence-space gives the impression that only a small number of the feasible range of molecular forms is currently extant, and that bio-molecular evolution is at a very early stage in its history. The picture is radically different, however, if we take into account the spatial arrangements of these sequences in three dimensions (Andrade 2000). The picture is now one of a shape-space which is virtually overflowing: newly evolving molecules must deform into complicated 3D-shapes to avoid atomic overlap. This has important implications with respect to any attempted distinction between living and non-living entities, and consequently to a style-of-emergence-based differentiation between “real” and “artificially” living systems. We will look at this in Paper II.
However, a second, somewhat softer, more directly-structural distinction between living and non-living systems can be developed on the basis of model-level richness. Upscaling in (extremely) non-living systems never provides representations or phenomena whose richness is more extensive than that of the preceding structural levels. Upscaling in (extremely) living systems, however, ultimately creates more complex, richer levels. Our own species’ evolution of a technological society is a case in point. In common with any attempt at formal categorization of natural phenomena, there is of course also a group of questionable systems whose properties fall between the categorical extremes, in this case many of those with chaos-related dynamics (e.g. hurricanes).
4. BIRATIONALITY AND ECOSYSTEMIC-DEPENDENCE
On closer examination, the generalized complementary hierarchical system illustrated in Figure 3 can be decomposed into two interleaved scaled level-systems, one corresponding to the Newtonian potential wells, the other to the inter-level complex regions (Figure 9) (Cottam, Ranson and Vounckx 1998b, 1999a, 1999b, 2000a, 2000b, 2001b). Each system then constitutes a progressively-changing assembly of models which is related to a specific style of rationality, and the two rational styles are themselves complementary.
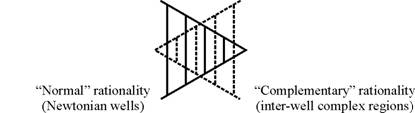
Figure 9. Decomposition of the generalized hierarchical system into two complementarily-rational representational assemblies.
From a viewpoint located in the Newtonian-well system, members of that assembly operate within a logically-inclusive manner, which may be associated with a “choose a problem-solution, test it in context, and update to reduce misfit” strategy [1] (and consequently with a use of conventional probability), while from that same viewpoint, members of the other assembly operate within a logically-exclusive manner, which may be associated with a “all you can do in the absence of complete information is to reduce the extent of the domain which may contain a/the problem-solution” strategy [2] (and consequently with a use of Dempster-Shafer probability - Dempster 1967; Shafer 1976).
From a viewpoint located in the complex-region system the same description holds, but now “what is inclusive” corresponds to “that which appeared to be exclusive” from the complementary Newtonian-well viewpoint. Each Newtonian level is paired with a complex precursor layer (Figure 10). At any particular scale, there are now two complementary representations. Not only is there a Newtonian-well form (as we would expect), but there is also a representation associated with its complex precursor. Starting from the left hand side of Figure 9 (or Figure 10), explicit representational information-content reduces with each step across the Newtonian-well assembly, while implicit (hidden) representational information-content increases with each complex-layer assembly step. Surprisingly, the information we previously presumed lost at a specific scale through the rational reductions from left to right in the Newtonian scheme is still locally present in the similarly-scaled precursor layer, whilst (apparently) still remaining inaccessible to operations within the Newtonian-style of rationality.
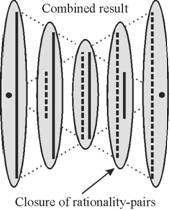
Figure 10. Pairing of the scaled Newtonian-wells with their co-scaled complex precursor layers.
At a specific scale, each of the two representations constitutes a rational ecosystem for the other: the Newtonian form exists within the rational constraints of its associated complex layer: the complex layer exists within the rational confines of the Newtonian one. It is (more than) interesting to note that this appearance of a birational structure corresponds closely to the bi-vectorial quantum-holographic solution adopted for NMR visualization problems (Schempp 2000), and to a quantum-holographic derivation of the double helix as the only viable format for reliable physical information replication in a 4D (3D+t) universe (Schempp 2002). Adoption of Karl Pribram’s (2001) proposal of a quantum physical basis for selective learning leads to a similar neural conclusion, namely that learning requires two complementary processes for its completion, only one of which is provided by the more usually-described neuronal network operations.
5. HYPERSCALE SYSTEMS AND AUTONOMY
The different levels of a unified hierarchy must of necessity communicate between themselves to maintain overall correlation. However, as we pointed out earlier, that communication must be circumscribed to avoid collapse of the hierarchy, and a balance must therefore exist between level (en-) closure (leading to autonomy) and inter-level dependency. Effectively, the inter-level complex regions provide support for (and constitute) inter-level autonomy/dependency-negotiation processes. A nice example of this is given by John Collier (1999), who proposes that the human brain cedes bio-support autonomy to the body in order to gain information-processing autonomy, and that both of them are in this way partially autonomous of/dependent on the other. The major challenge in understanding the operation of scaled (hierarchical) systems is to construct context-relevant representations of this autonomy/dependency-negotiation, most particularly as the complex region between levels is fractal in every possibly imaginable manner (Cottam, Ranson and Vounckx 1999b).
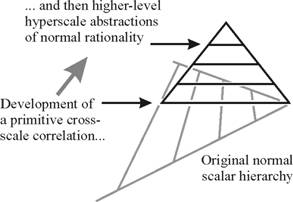
Figure 11. The superposition of a hyperscale (cross-scalar) hierarchy on the initial Newtonian-well scalar hierarchy.
The simplest model of the relationship between levels of a unified hierarchy is just that: “it is unified” – a binary model. We will need to do a lot better than that! If hierarchy is a fundamental element of nature, then models of hierarchy must themselves be hierarchical. It is useless to model complex context-dependent processes from a platform which is less complex and non-context-dependent (i.e. a scale-free formal rationality). First of all we need to construct a model which can evolve, and then apply it not only to the modelling-target, but also to the way we think about or rationalize the model. In our current context, therefore, we must permit the modelling process (c.f. Figure 3) itself to be hierarchical, but now we are moving from right to left through the structure: on the basis of the binary model (“it is unified”) we can search for a more comprehensive representation, and so on iteratively (and, in fact, recursively). In doing so, we develop a hierarchical scaled rationality (Cottam, Ranson and Vounckx 1999b) by a combined top-down and bottom-up procedure (or rather, as is usual in an ecosystemic system, from the middle outwards).
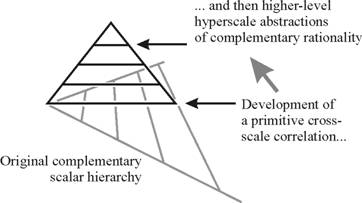
Figure 12. The superposition of a hyperscale (cross-scalar) hierarchy on the complementary complex-layer scalar hierarchy.
To cut a (very) long story short, adoption of this approach results in the development of a hierarchical structure of (partially en-) closed cross-scale layers, superimposed on the original scaled hierarchy (see Figure 11). As this superimposed structure now consists of a multiplicity of scaled representations of the unification of multiple scales, they can best be referred to as hyperscalar levels, which correspond to scaled abstractions of the “phenomenon” we usually refer to as understanding, as the process of their development can be related to learning.
As a simple example of this relationship we can imagine a digital computer[vii], which is constructed of sub-units (e.g. memory), which are in turn composed of logic gates, which are fabricated from transistors, … Different abstract levels of “understanding” of this system’s form can be referred to, each one of them at the very least relating to a specific level, to its relationship with a higher one and to its “construction” from a lower one (thus also providing the three levels of understanding required by Stan Salthe’s (1985) prescription for hierarchy).
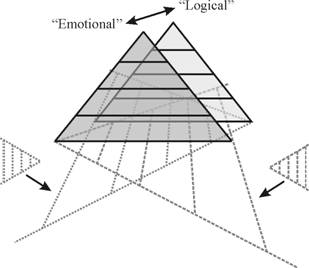
Figure 13. Illustration of progressive decoupling of the complementary hyperscale hierarchies with abstraction.
In a birational co-ecosystemic system, this approach must clearly also be applied to the complementary hierarchy (see Figure 12). To complete the picture at this order of description we must also remember that the initial complementary Newtonian-well and complex-layer hierarchies are intimately correlated at corresponding scales. The lowest levels of the two new hyperscale hierarchies will also be closely coupled and complementary, although less so, but as we move upwards towards higher levels of hyperscale abstraction they progressively decouple (Figure 13).
We believe that these two nominally complementary co-ecosystemic rational systems are related to the neural co-evolution of “logic” and “emotion”, and to their inter-dependent usefulness in breaking information-processing logjams (Cottam, Ranson and Vounckx 2001b).
6. AUTOCREATIVE HIERARCHY
While, for the sake of simplicity, we have described these scalar and hyperscalar hierarchies mainly as externalist constructions, we believe that they provide a helpful description of the way that natural systems of all kinds “self-organize” via internal(ist)/external(ist) negotiations between non-commutative representational and creational logics (Cottam, Ranson and Vounckx 2001b). Natural hierarchical levels appear really (ontologically) to exist, and are not just (epistemological) figments of our observational imagination. If this is the case, then it becomes necessary to re-evaluate rather carefully the relationship we habitually presuppose between the stabilization of locally-scaled levels in both living and non-living systems and our conception of the place of awareness or consciousness in the scheme of things (Weber 1987; Cottam, Ranson and Vounckx 1998c). This, of course, possibly opens up a somewhat unwelcome can of worms.
As we pointed out earlier, the majority of information which is transported upscale in a hierarchical system is related to order and not to novelty, although it is the novelty resulting from inter-level complex autonomy/interdependence negotiations which ultimately defines the differentiation between hierarchical levels. “Emergence” experiments often exhibit very little in the way of real novel cross-scale effects, and level differences are often attributable to unintended or un-noticed inter-level rule-transport (Cottam, Ranson and Vounckx 2002a), whose dominance is concealed in the complications of the system. This gives rise to the observation of emergence of higher-level properties which, however, result uniquely from ordered inter-level information transport (Cottam, Ranson and Vounckx 2000a).
We believe that the waters of self-organization are seriously muddied by a lack of distinction between “quasi-emergent” forms which are related to unawareness or computational incompleteness and those (Cottam, Ranson and Vounckx 1998a) whose existence derives uniquely from non-formally-modellable co-ecosystemic complex autonomy/dependence negotiations. Most particularly, we do not see any use for the design or construction of “artificially alive” entities, systems or their descriptions which leave out co-ecosystemic evolution, whether in their (included) relationships with their (excluded) environment or in their internal workings (Cottam, Ranson and Vounckx 1998c). It would seem that all aspects of “living” constructions should be co-ecosystemic, or they risk being of restricted value as simulations or derivatives of living systems, most particularly if the target is to establish grounding for future artificial life applications, for example in the fast-growing domain of collaborative robotics (Cottam, Ranson and Vounckx 2002b).
REFERENCES
Andrade, E. 2000. From External to Internal Measurement: a Form Theory Approach to Evolution, BioSystems 57:49-62.
Antoniou, I. 1995. Extension of the Conventional Quantum Theory and Logic for Large Systems. Aerts, D., and Pykacz, J. eds. Quantum Structures and the Nature of Reality: the Indigo Book of the Einstein meets Magritte Series. Dordrecht: Kluwer Academic.
Collier, J. D. 1999. Autonomy in Anticipatory Systems: Significance for Functionality, Intentionality and Meaning. In Proceedings of Computing Anticipatory Systems: CASYS'98 - 2nd International Conference, AIP Conference Proceedings 465, 75-81. Woodbury, New York: American Institute of Physics.
Cottam, R.; Ranson, W.; and Vounckx, R., 1997. Localisation and Nonlocality in Computation. Holcombe, M., and Paton, R. C. eds. Information Processing in Cells and Tissues, 197-202. New York: Plenum Press.
Cottam, R.; Ranson, W.; and Vounckx, R. 1998a. Emergence: Half a Quantum Jump? Acta Polytechnica Scandinavica 91:12-19.
Cottam, R.; Ranson, W.; and Vounckx, R. 1998b. Diffuse Rationality in Complex Systems. Interjournal of Complex Systems Article #235.
Cottam, R.; Ranson, W.; and Vounckx, R. 1998c. Consciousness: the Precursor to Life? In Proceedings of the Third German Workshop on Artificial Life, 239-248. Thun, Germany: Verlag Harri Deutsch.
Cottam, R.; Ranson, W.; and Vounckx, R. 1999a. A Biologically-Consistent Diffuse Semiotic Architecture for Survivalist Information Processing. Proceedings of the Seventh World Congress of the International Association for Semiotic Studies: Sign Processes in Complex Systems. Technical University of Dresden, Germany. Forthcoming.
Cottam, R.; Ranson, W.; and Vounckx, R. 1999b. A Biologically Consistent Hierarchical Framework for Self-Referencing Survivalist Computation. In Proceedings of Computing Anticipatory Systems: CASYS'98 - 2nd International Conference, AIP Conference Proceedings 465, 252-262. Woodbury, New York: American Institute of Physics.
Cottam, R.; Ranson, W.; and Vounckx, R. 2000a. Executing Emergence! In Proceedings of the Fourth International Conference on Emergence, Complexity, Hierarchy and Order. Washington, DC: ISSE. Forthcoming.
Cottam, R.; Ranson, W.; and Vounckx, R. 2000b. A Diffuse Biosemiotic Model for Cell-to-Tissue Computational Closure. BioSystems 55:159-171.
Cottam, R.; Ranson, W.; and Vounckx, R. 2001a. Artificial Minds? In Proceedings of Forty-Fifth Annual Conference of the International Society for the Systems Science, #01-114, 1-19. Pacific Groove, CA: ISSS.
Cottam, R.; Ranson, W.; and Vounckx, R., 2001b. Cross-scale, Richness, Cross-assembly, Logic 1, Logic 2, Pianos and Builders. Proceedings of the International Conference on the Integration of Information Processing. Toronto, Canada: SEE. Forthcoming.
Cottam, R.; Ranson, W.; and Vounckx, R., 2002a. Self-Organization and Complexity in Large Networked Information-processing Systems. Proceedings of the Fourth International Conference on Complex Systems. Nashua, NH: NECSI. Forthcoming.
Cottam, R.; Ranson, W.; and Vounckx, R., 2002b. Lifelike Robotic Collaboration Requires Lifelike Information Integration. Proceedings of the Performance Metrics for Intelligent Systems Workshop. Gaithersburg, MD: NIST. Forthcoming.
Dempster, A. P. 1967. Annals of Mathematical Statistics 38:325-339.
Langloh, N.; Cottam, R.; Vounckx, R.; and Cornelis, J. 1993. Towards Distributed Statistical Processing: A Query and Reflection Interaction Using Magic: Mathematical Algorithms Generating Interdependent Confidences. Smith, S. D. and Neale, R. F. eds. Optical Information Technology, 303-319. Berlin, Germany: Springer-Verlag.
LeDoux, J. E. 1992. Brain Mechanisms of Emotion and Emotional Learning. Curr. Opin. Neurobiology 2: 191-197.
Pribram, K. 2001. Proposal for a Quantum Physical Basis for Selective Learning. In Proceedings of the Fourth International Conference on Emergence, Complexity, Hierarchy and Order. Washington, DC: ISSE. Forthcoming.
Salthe S. N., 1985. Evolving Hierarchical Systems. New York: Columbia U. P.
Salthe S. N., 1993. Development and Evolution. Cambridge: MIT Press.
Salthe S. N., 2002. Private communication.
Schempp, W. 2000. Quantum Entanglement and Relativity. In Proceedings of the Fourth International Conference on Emergence, Complexity, Hierarchy and Order. Washington, DC: ISSE. Forthcoming.
Schempp, W. 2002. Replication and Transcription Processes in the Molecular Biology of Gene Expressions: Control Paradigms of the DNA Quantum Holographic Information Channel in Nanobiotechnology. BioSystems. Forthcoming.
Shafer, G. A. 1976. Mathematical Theory of Evidence. Princeton: U. P.
Weber, R. 1987. Meaning as Being in the Implicate Order Philosophy of David Bohm: a Conversation. Hiley, B. J., and Peat, F. D. eds. Quantum Implications: Essays in Honor of David Bohm, 440-41 and 445. London: Routledge and Kegan Paul.
ENDNOTES