Autocreative Hierarchy II

Autocreative Hierarchy II:
Dynamics – Self-Organization, Emergence and Level-Changing

Ron Cottam, Willy Ranson and Roger Vounckx

The Evolutionary Processing Group

IMEC Brussels, ETRO

Brussels Free University (VUB)

Pleinlaan 2, 1050 Brussels, Belgium

evol@etro.vub.ac.be

©This paper is not for reproduction without permission of the authors.

Abstract

Natural systems are characterized more by the way they change than by their appearance at any one moment in time. There is, however, no self-consistent theory capable of ascribing the development of living hierarchical organisms to conventional scientific rationality. We have derived a generic model for the dynamics and evolution of natural hierarchical systems. This paper presents the resultant birational dynamics which may be attributed to a real hierarchy. We describe the nature of self-organization and of emergence in hierarchies, and the rationality which may be employed to move between scalar levels. We propose the use of diffusely-rational recursive Dempster-Shafer-probability to model inter-hierarchical-level complex regions, and consider its implications. The evolution of living from non-living systems is attributed to a change in the style of emergence which characterizes the appearance of new scalar levels.

1. Introduction

In an earlier paper[i], we have presented structural aspects of a model for the hierarchical development of large unified natural and artificially-alive systems. In this paper we will examine the contributive and consequent dynamical aspects of the model, and the structural-dynamic relationships.

As we pointed out in our introduction to AH-I, any definition of “large unified systems” in our sense depends fundamentally on the recognition that major nominally-different aspects of these systems are intimately coupled. Large unified systems can only exist as a partial negation of, or ambiguity in, their own states; we must in some way match this partiality with the descriptive forms we adopt. These considerations apply to the structure and dynamics of the systems themselves, and also to our discussion of them. Although, for the sake of clarity, and in the manner most usually employed in reductionist scientific investigation, we have split our discussion into two parts, namely “structure” and “dynamics”, the two are functionally inseparable. Of necessity, a number of hints relating to hierarchical dynamics appeared in AH-I, and further structural aspects will appear in this paper.

We have left until now any major reference to the character of the relationship between structure and dynamics. Following common cultural bias, we first looked at the structure of hierarchical systems as if it were an independent aspect – as if the systems could be frozen in time. It is less attractive to describe dynamics in a similar “frozen” manner, as we habitually think not of “doing…”, but that “something does…”. Consequently, in this paper we will adopt the hierarchical form of supposing that dynamics consists of two subsidiary complementary parts, namely structure and its counterpart process. It should be noted that simplification of a binary complement can lead to binary orthogonality, or by more extreme reduction leads to a pair of opposites. Structure and process are complementary in neither of these simplified senses, but in that indicated by Niels Bohr: “The opposite of a correct statement is a false statement… but the opposite of a profound truth may well be another profound truth.” In places where we do not wish to split dynamics into these two reductively-separate aspects, structure and process, we will refer to the complement by the word struccess (Cottam, Ranson and Vounckx 1999c).

Our major aim in this paper is to relate the dynamics of natural and artificial systems to the hierarchical scheme we have described in AH-I, and to add flesh to the bones of the birational co-ecosystemic architecture. A subsidiary target is to redefine use of the word emergence to be more consistent with the necessarily less-than-formally-rational nature of hierarchical inter-level complex regions. To do this, we also need to address use of the word complex in such a context, and the place of quantum mechanics and traditional physical viewpoints in a self-consistent overall hierarchical scheme. To be useful, such a framework must be capable of including in a natural manner all possible scales of the near-to-equilibrium correspondences confirmed by formally rational science, from the environmental dimensional coupling of super-strings (Green, Schwarz and Witten 1987) to the emission of energy from black holes (Hawking 1975). Our formulation appears to be reliable across scales in this manner, and its birational nature is consistent with quantum holography[ii], and also, therefore, with Einstein’s gravitation theory at the macro scale (Schempp 2000).

2. The Problem of Self-organization

The ubiquitous, almost magical transition from “a set of components” to “a unified system” is possibly the most fascinating aspect of our natural environment, especially as witnessed in the realm of (living) biological organisms. A major part of artificial-life (and other) investigations is concerned with the observation and origins of self-organization in artificially-established systems. This is, however, rather a slippery subject, as many, if not most reported examples of “self-organization” are primarily “investigator-organized”. The emergence of new properties on changing level in a hierarchical assembly is often more attributable to un-noticed inter-level transformation of pre-imposed rules or initial experimental conditions than to self-organization.

Figure 1. A fish, or not a fish?

The following is a simple example of this style of misconception (as usual, exposition demands an unusually simple form where error is obvious – more commonly it would be less so, but this is in fact a real example from an artificial life conference presentation). Twenty “turtles” are all placed at “zero” in a 2-dimensional computer-screen environment. They are all instructed to move 10 “distance units” in a random direction away from zero. Result: a circle emerges by “self-organization”. The reader will (almost) certainly have noticed error number 1: the initial conditions and instructions pre-define the final circular arrangement of the “turtles”. Error number 2 is slightly less obvious: there is in fact no emergent circle in the system being investigated, only a (circular) arrangement of coloured dots. The circle is only present in the observer’s mind: somehow we have sneaked ourselves into the “closed” experimental system (Cottam, Ranson and Vounckx 2002a).

This inadvertent observational-inclusion of the spectator in a (non-QM) nominally formally-bounded environment is pervasive. Microsoft kindly provide Figure 1 in their clip-art files, illustrating that a “fish” on a computer screen is not, in fact, real. In fact the situation is far worse than that: there is no image of a fish at all on the computer screen, only a set of coloured dots in positions which are defined by a technical system conceived to transmit arbitrary two-dimensional patterns between locations – the “fish” is created in the mind of the observer. Again, there is a degree of confusion between the two nominally separate systems of “the experiment” and “the observer’s mind”. Much of the power of observed self-organization in (especially computational) artificially-established systems is due to our own neural capabilities (Cottam, Ranson and Vounckx 2000a).

It is, however, necessary to be somewhat circumspect in insisting that there should be no formally rational link between underlying properties and emergent ones, as in general not all the properties of formal systems are themselves formal (Collier 2002). We will address this issue more extensively in a later section of the paper.

A further difficulty in this area is the attribution of characteristics which we expect or presume to be present on the basis of limited information. In a survival-computational sense (Cottam, Ranson and Vounckx 1999a) this quasi-symbolic response is a natural feature of our neural processes, enabling rapid reaction in critical situations (LeDoux 1992). Unfortunately, it can also be entrained by lack of attention to contextual information or over-orientation towards an experimental target. A classic example of this (also from conference proceedings) is the unwarranted imposition of categories: “Why do seagulls nest on tall buildings? … because they have created a category which includes cliffs and skyscrapers” (and not, maybe, that the reduced model they are using leads them into erroneous identification?).

If we ourselves are led into error by the styles of logic we use or misuse, how is it that our surroundings remain the same if we close our eyes and then reopen them? Nature apparently makes a much better job of things than we do…

3. Communication and Structural Dynamics

We pointed out in AH-I that “a localized entity in a global environment must not only be isolated from it but must also communicate with it”. Communication must be partial, not only with all perceptual scales of (to some degree all) other entities, but also with all perceptual scales of the entire assembly of entities.

Schematically, we can model an entire local-to-and-from-global system as a multi-dimensional extension of the scheme presented in AH-I (see Figure 2), where different entities are represented as different “left-to-right” dimensions (note that for clarity the different scales of the individual entities have been left out of the illustration). Should we now be referring to a large number of clearly-defined selectable (“yes or no”) parallel inside-to-outside channels linking any general entity to its environment? We think not: this suggestion seems not only to be the result of a pre-formed (Newtonian) world-view, but also to leave quantum mechanics completely out of the picture, and to simply convert the problem to one at a smaller scale. Although a multi-specified channel model can reasonably well match many formally modelled monoscalar inter-communicational situations (e.g. biological cell membranes), it is not sufficiently dynamically context-dependent or versatile to be used as a general representation. Rather than grounding our model on digitally-partial links (and therefore on linear superposition), we should refer it to analog-partial coupling (and therefore QM superposition) and digitally-partial links in a context-dependent manner. In the framework we have presented in AH-I, whose defined levels are located at a multiplicity of intermediate points between perfect (digitised) localization (which may be related to classical probability – Cottam, Ranson and Vounckx 1998b) and (analog) nonlocality[iii] (which may similarly be related to Dempster-Shafer {D-S} probability, with P_L= 0 and P_U= 1 – Dempster 1967; Shafer 1976; Cottam, Ranson and Vounckx 1997a, 1998b) we choose to base partial inter-entity communication on a multiply-recursive D-S probability (Cottam, Ranson and Vounckx 1998b, 1999b). Each entity (dimension) is represented by a recursive D-S probability, whose recursivity increases (in the operational manner of a Lyapounov exponent) between spatio-temporal localization and nonlocality.

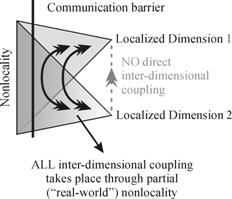
Figure 2. Illustration of possible and forbidden communication routes through a 2-dimensional (i.e. 2 entity) system.

To obtain inter-dimensional (inter-entity) interactions which increase progressively from a complete set of isolated singularities (at the right-hand side of Figure 2) to a single QM-style superposition (at the left-hand side of Figure 2) we allow the recursive D-S probability of every individual dimension to interact, again recursively, with all the others. In the sense of AH-I, where hierarchical levels were referred to as scaled forms of a particular style of rationality, this technique provides a framework within which varyingly-diffuse rationality (Cottam, Ranson and Vounckx 1998d) can be located. Both the scalar-location of an entity within the global “phase-space”, and its dynamic interactions with all other extant entities and with different scales of the entire assembly can now be instantiated and updated in a Newtonian-QM-consistent context-dependent manner. The attribution to entities of a local (scaled!) “intelligence” now sets the stage for using the framework to provide a biologically-consistent setting (Cottam, Ranson and Vounckx 2000b) within which the dynamics of a large unified system of multiple partially-autonomous agents may be modelled.

In essence, this framework is an embodiment of the evolutionary natural semiotic (ENS) (Cottam, Ranson and Vounckx 2002b) approach to representing and creating coupled multiply-scaled-agent (CMSA) systems (Cottam, Ranson and Vounckx 2001b). It provides support for the configuration of semiotic (Taborsky 1998, 2002) and biosemiotic (Hoffmeyer and Emmeche 1991a, 1991b) architectures in more-or-less formal or biological media. In our description, the emergence[iv] of both stabilizing and unstable localized higher-level entities, from quantum quasi-particles to perceptions to living entities (Cottam, Ranson and Vounckx 1998a) takes place in an abductive manner (Taborsky 1999), while (non-commutative) re-correlation of these emergences with their lower parent levels takes place through complementary subductive processes. Abductive emergence into a Newtonian well takes place from its associated locally-specified underlying complex level (Cottam, Ranson and Vounckx 2000b) (Figure 3), whose dimensionality is subductively related to that of the emergent entity.

Both these transitions require the establishment of negotiative dynamic solutions to internal-external representational mismatching, within which purely internalist or externalist points of view are destructively reductive, and the negotiation is similar to the process we go through when we try (internally) to model some (external) physical phenomenon, without having a firm grasp on its causal nature[v] (N.B. causality is how real transitions occur: rationality is our always hypothetical attempt at understanding why they occur – Cottam, Ranson and Vounckx 1999b).

For the sake of simplicity, we are considering all the scalar hierarchies to which we refer in this paper to be synchronous, in that the “centres of gravity” of all of their individual scaled representations are at the same location in the global phase-space. We will not attempt to deal with more interesting non-synchronous systems in this paper, other than to note that their interactions are probably relevant to conceptual creativity (Cottam, Ranson and Vounckx 2000a). It is worth noting in passing that this entire structure is based originally on a computational architecture designed to provide multi-scaled stimulus-reaction, and therefore entity survival-promotional computation, in a partially nonlocal optical information processor (Langloh, Cottam, Vounckx and Cornelis 1993).

4. Emergence

Unfortunately, the many different uses of the word complex makes it difficult for us to distinguish between two major characteristics of emergent hierarchical systems, namely (in our terms) complication and complexity. We can start off with an (approximate) computational formulation: if simple means “easy to compute”, then complicated means “more difficult to compute”, and complex is ultimately incomputable. The dynamics of the Newtonian wells in a hierarchical scheme run nominally from simple to complicated (not forgetting the difficulty of the Newtonian three-body problem – which is related to the direct/indirect link network specification we presented in AH-I). While complication can have a purely static structural interpretation, the sense of complexity which we wish to capture is always dynamic, involving struccess. Deriving from Rosen (1985), Mikulecky (1999) has neatly expressed an overall sense of the complex which we can accept, as

“Complexity is the property of a real world system that is manifest in the inability of any one formalism being adequate to capture all its properties. It requires that we find distinctly different ways of interacting with systems. Distinctly different in the sense that when we make successful models, the formal systems needed to describe each distinct aspect are NOT derivable from each other.”

… but we need to go somewhat farther in this case, as our intention is to reduce the class of systems represented by complex to a minimum[vi] “core of dynamic complexity”, which we believe would in neural terms correspond to Tononi and Edelmans’ (1998) “core of consciousness” (which is dynamic in both character and neural location)[vii].

“Complicated” can best be used to describe systems which can only be unified by a data-destructive procedure which corresponds to [digital approximation]ⁿ, or “reduction-to-a-simpler-model” ad absurdium, and which results in a single binary representation of “true” (or “false”, which seems a somewhat self-destructive argument!). Complicated systems are only epistemologically unified. “Complex” is best used to describe systems which are naturally (ontologically) unified, and not those which are only “unified” in our eyes (or models). A complex system will always have a unified character (to some non-unitary degree of approximation): not so for a complicated system.

We now have descriptive tools available which we can apply to the various structural aspects of hierarchy. Each of the Newtonian wells is a single-scale representation of the system; the entire system is approximately described in terms of the (recursively) functionally most important scale at that scale[viii]. As such, each well is structurally complicated, and its dynamics are only complex in that the processes involved are incomplete-complex (e.g. in the mathematical description of a Newtonian three-body problem there are insufficient conserved quantities to solve the system of equations: the structure is incomplete-complicated, so its dynamic representation is incomplete-complex[ix]).

There is a clear link between these aspects of complexity and the “inadvertent observer-inclusion” to which we referred earlier: artificially constructed complicated systems are not naturally unified: their apparent unification depends on our (extra-systemic) neural power (as did unification of the circular pattern of spots, or the image of a fish, which we gave earlier as examples the erroneous announcement of emergence). Clarification of the sense of emergence which we seek depends on just this: real emergence is ontological (at least), although it may entrain epistemological forms. Hierarchy, emergence and struccess are coupled in the same way as the elements of “large unified system”: they coexist in a cooperative-competitive mode (Cottam, Ranson and Vounckx 1999b), which depends on a delicate balance between enclosure and process closure.

The best paradigm for real emergence is provided by the electronic quantum jump between energetic levels of an excited atom. Emergence does not proceed “off its own bat”, independently of the surroundings. It is the reaction of a partially enclosed system (e.g. a level of a hierarchical system) to change in its environment. Super-cooled liquids crystallize when their container is shocked, or when the temperature falls even farther. However, it should not be presupposed that quasi-isolated entities have infinite lifetimes. As we indicated in Figure 2, perfectly isolated entities cannot communicate: we would not even be aware of them. The lack of isolation of real localized entities makes them susceptible to global constraints, and gives them limited viability. Entities decay! They must do so as a route to local-to-and-from-global correlation (Cottam, Ranson and Vounckx 2000a). The atomic electron is a case in point: thus the inscrutable nature of its inter-level quantum jump. First the electron decays away; this leaves the atomic system in an incompletely-stable state, provoking the re-emergence of an (or the?[x]) electron, either in the same state or, if atomic conditions have changed, in a different state (Cottam, Ranson and Vounckx 1998a). It should be noted that here we are referring to a generic quantum jump: whether as observers we notice any difference depends on whether atomic conditions prescribe that there “should be one”. For a particle which we observe “moving along a trajectory” the situation is similar. In that the “particle” is by definition “localized”, it has incomplete knowledge of its relationship to global conditions unless it decays back into the nonlocal state “to check”. The phenomenon we describe as movement then corresponds to the particle’s regular re-emergence at sequentially different locations along the trajectory[xi], consequent on its own observation (Matsuno 1996) of the local implications of global conditions (Cottam, Ranson and Vounckx 1998a).

This style of oscillation in-and-out of localization and nonlocality is the ubiquitous stabilizing mechanism of “real” hierarchies. It autonomously takes place directly between any Newtonian well and its paired complex layer, and indirectly between any and all of the different scalar levels through interactions with other non-paired complex layers. The selection of which parts of the global phase-space will be occupied by Newtonian wells is the evolutionary result of this process over the lifetime of the system: a current configuration of the overall scalar-well/complex-layer assembly defines the future of the scalar-well/complex-layer configuration, in the same way that the injection of “evolution” breaks down the conundrum of chicken-or-egg precedence.

Part of the character of a new level which emerges in an evolving hierarchical system is defined “bottom-up” by information which is transmuted from lower levels through this mechanism of response to local-global imbalance. A further “top-down” response-contribution results in the level’s elements being slaved to higher levels. In this way the level’s character is uniquely determined in the hierarchy, and its establishment can be described in terms of a set of order parameters, which can be used to formulate a parametric model of the new level (Haken 1984). Slaving of the constituent elements of a lower level is defined not only by the next higher level, but indirectly by influences from every level higher up. This means that the individual constituent elements at a very low level in an extensive hierarchy will show far more self-similarity than elements at a level which is nearer to the hierarchy's summit. As an example of this, we can consider the differences in differentiation between elementary particles, as low level elements of the biological hierarchy, and cells, which are much higher up. In a hypothetical, much earlier, less evolved form of the universe, the hierarchical level associated with elementary particles will have corresponded approximately to the summit of evolution, and we would expect to find far more differentiation between individual particles, as their degrees of freedom would be far less slaved into their version of the formal quantum numbers we now use to represent them. In the extensive hierarchy within which we are now aware of elementary particles, they exhibit very little, but very formalized differentiation. Conversely, biological cells, which are functionally very close to the summit of the biological hierarchy we now experience, are endowed with an enormous number of ill-formalized degrees of freedom, and consequently they exhibit a very high degree of differentiation, even to the extent of developing hierarchical differentiation, with for example many quite different kinds of neuron. (It should be noted that cumulative slaving down through many levels of a hierarchy will result in nonlinear differentiation of slaving throughout the hierarchy: towards the top there will be far less inter-level differentiation than lower down. Consequently, although there are many levels higher than that of single cells in the biological hierarchy, their slaving remains comparatively weak.)

Our basic paradigm for emergence, then, is the second half of a quantum jump (Cottam, Ranson and Vounckx 1998a), or more specifically the appearance in a provisionally stabilized form of a system’s local-to-and-from-global self-correlating reaction to external stimulus or constraint: it is the process by which a system corrects its temporarily out-of-equilibrium local-global causal-conservative balance. Emergent struccess is naturally to some extent apredictable, as well as being to a degree necessarily unpredictable in the face of insufficient local access to global data (caused by the speed-of-light limitation). In quantum mechanics this unpredictability makes itself apparent in Heisenberg’s Uncertainty Principle, or as Feynman’s Summation Over All Paths, to both of which it is equivalent at that scale, but only if the direct inter-formal-parametric coupling is zero as indicated in Figure 2 (Cottam, Ranson and Vounckx 1997b).

One last aspect of emergence we wish to examine is the often repeated formula: “the whole is more than the sum of the parts”. This makes little or no sense in a birational hierarchical system, where at each scale information is distributed between two separate layers, only one of which is normally accessible to dynamical processes. More concretely, as we move through a hierarchy towards higher (larger scale) representations we find a progressively reducing summation of explicit plus implicit information in consecutive scaled layer-pairs. This is a rather normal consequence of evolutionary emergence: as Root-Bernstein and Dillon (1997) point out, “... at each step of sub-assembly, huge numbers of possibilities are eliminated”: evolutionary processes are to some extent informationally-compressive in their progression. Consequently, it makes little sense to maintain that emergence is equivalent to a “free lunch”. More to the point, there is an informational configuration exchange between the two complementarily-rational members of associated scalar-level pairs on moving from one scale to another, such that the new combination of descriptive order parameters may result in apparently very different characteristics appearing at different scales. This configuration exchange has the character of an autonomy negotiation (Conrad 1983, Collier 1999b) between the scalar-level pairs, which involves realignment of the explicit information which appears in the Newtonian well and the implicit information associated with the complex layer. To all intents and purposes, the whole is always less than the sum of the parts!

5. Level-changing

A prime reason for investigating hierarchical artificially-alive schemes is to facilitate the extension of artificial system scale towards that of living organisms. Artificially-alive systems will, of course, experience the same problems as those which biology has already confronted, and already solved - precisely through its adoption of hierarchical forms. Unfortunately, the construction of formally-modellable inter-scale transitions will be of little or no help in this enterprise, not only because a real formally-coupled large multi-scale system would quickly grind to a halt as a consequence of the unavoidable communication-speed restriction, but that it is precisely the inter-scalar complex regions which “take up the slack” that is always associated with less-than-perfect environmental reactions which involve various incompletely-coherent scalar representations of one and the same entity.

The adoption of multiply-recursive D-S diffuse rationality (Cottam, Ranson and Vounckx 1999b), which we propose as an initial step in modelling the hierarchical inter-scalar complex regions, provides for a continuous operational domain which extends between formal rationality, corresponding to perfectly defined values, and nonlocality, corresponding to Stan Salthe’s “ultimate vagueness”, through differing intermediate degrees of diffuseness[xii]. All real dimensional evaluations are then associated with a degree of inter-dimensional “measurement” imprecision, in a manner consistent with, but in scale more general than, a Heisenberg uncertainty. A major result of this modification of formal rationality is that the otherwise always-present risk of complete analytic failure in far-from-equilibrium phase-space regions is alleviated. From a survivalist point of view, an evaluable degree of “normal” computational uncertainty is much more acceptable than “normally” high accuracy and occasional disaster. Small errors are more user-friendly than large ones!

Moving between Newtonian levels from the left-hand side of Figure 2 (or Figure 4 of AH-I) towards the right-hand side is equivalent to compressing explicit information into new reduced formats: information is lost. The observation of level emergence corresponds to witnessing this process. Transit back towards the left-hand side is far less obvious, as location from a given scale of other levels which are farther towards its left is distorted by the lack of complete information. The major problem is to see how to model not only the inter-scalar regions (as we suggest above), but to model transitions through these regions, whose necessarily complex nature defies straightforward representation.

The key to solving this problem lies in recognition of two aspects of the birational hierarchy illustrated in Figure 3. Firstly, although the style of rationality through each of the rational subsystems remains the same, the degree to which it is implemented changes across the hierarchy. The Newtonian well assembly follows the “normal” style of rationality we would expect, but while at the right-hand side of Figure 3 it is understandable as simple causality, at the left-hand side it constitutes a digital simulation of quantum-mechanical superposition. Similarly, the complex (complementary) assembly exhibits quantum mechanical rationality at the left-hand side and QM-simulation of simple causality on the right[xiii]: the localized/delocalized natures of classical/quantum-mechanical superpositions appear both in analog and digital forms. This scheme matches Karl Pribram’s (2001) two-stage quasi-QM model for learning: not only is there “normal” neuron-interaction superposition, but the quasi-wave collapse he proposes corresponds to the high-level discrete-channel information distribution necessary to simulate quantum superposition.

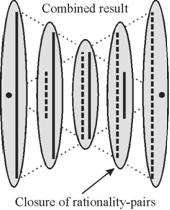
Figure 3. Closure of rationality-pairs in a birational system: Newtonian levels – full lines; complex levels – dashed lines.

We can now propose the form of a modelling technique for level-changing. Each “normal” scalar-level is associated with a QM-like complementary layer, which acts as a local rational ecosystem for it by containing all of the (evolutionarily-dumped) missing information which would otherwise enable complete system description at that scale. Although the evolutionarily-reduced “normal” level at any scale contains insufficient explicit information to accurately target other possibly-stable differently-scaled phase-space niches (and this is especially true for high-level emergences), the informational content of the combination of both members of the scalar pair does fulfil this requirement (the birational system corresponds in fact to a coherently-multi-scalar “hidden variables” model). If it were not that the QM-like contents are inaccessible to “normal” rationality, the trick would be to first integrate both scalar-pair contents, and then search for a new niche. In quantum teleportation, as a normal preparation for performing QM error correction, ready-to-be transmitted qubit information is supplemented by the addition of extra coded dimensions. Possibly-deformed information at a later stage in the transmission can be corrected by reference to these extra dimensions without looking at their contents! It turns out that the operation we require for hierarchical inter-level transit is a high-level generic form of this process (Cottam, Ranson and Vounckx 2001b). Performance of a transit towards the right-hand side of the birational hierarchical system of Figure 3, from any intermediate “normal” scalar-level, entails first accessing its parent complex layer (which is situated to its left) and afterwards searching for a stable niche (towards the right): per sinistra ad dextram! [xiv]

This specifically dynamic phenomenon appears to be a principal aspect of (context-sensitive) complementary systems: any current reductionist representation is insufficient to successfully achieve dynamic local-global re-correlation on its own, without first accessing the complete locally-scaled complementary representation. Its character is linked to the mathematical differentiation of a binary complement (Cottam, Ranson and Vounckx 2000a), but the nature of that relationship (or how to perform such a mathematical operation) is as yet unclear.

6. Living versus Artificial Systems

We should not expect the physics of living systems to be “more of the same” of what we have already seen in physics-as-describing-near-equilibrium-systems: it may be very different. Indications of this disparity are starting to appear: the traditional rejection of large-scale quantum coherence in normal-temperature biosystems is currently under re-evaluation, with the proposal and modelling of quasi-QM systems related to those which appear in the complex layers of this paper (see, for example, Pribram 1991, 2001; Farre 2002). Unexpected effects are also appearing in relation to the attempted application of thermodynamics to open living systems. Notably, Koichiro Matsuno (2000) has reported quantal emissions from Actomyosin AT-Pase activity in the presence of ATP molecules which indicate effective temperatures of 1.6 x 10^-3 K! Are these effects fundamental to life? In that they are associated with both biological scaling and powering: probably. Is it possible to establish highly-scaled artificially-alive hierarchies without adopting the birational approach we propose in AH-I and this paper? We clearly believe not. Evidence of quantal effects in biosystems suggests that at least some form of integration of classical and QM rationality is needed, and that in conjunction with hierarchy.

A last comment is specifically related to emergence, and the distinction we drew in AH-I between living and non-living systems on the basis of higher-level emergent richness. Andrade’s (2000) picture of a protein shape-space which is virtually overflowing supports our own view that living systems are also delineated from non-living ones by the style of emergence upon which they depend. Low-complication (non-living) systems exhibit only analog-to-digital emergence (from nonlocality to localization). Living systems have built on this by “inventing” an efficient extension, from complication into highly-structured-complexity (Cottam, Ranson and Vounckx 1999a), through the emergence of (analog) protein-folding from (digital) DNA.

Acknowledgement

The authors would like to express their gratitude to the participants of ECHO-IV (Odense, Denmark 2001) for their numerous responses to our request for help in resolving the per sinistra ad dextram aspect of hierarchical level-changing. Most particularly, we wish to thank Walter Schempp, for his most apposite remark: “While you were talking, I was thinking of quantum error correction”!

References

Andrade, E. 2000. From External to Internal Measurement: a Form Theory Approach to Evolution, BioSystems 57:49-62.

Collier, J. D. 1999a. Private communication.

Collier, J. D. 1999b. Autonomy in Anticipatory Systems: Significance for Functionality, Intentionality and Meaning. In Proceedings of Computing Anticipatory Systems: CASYS'98 - 2nd International Conference, AIP Conference Proceedings 465, 75-81. Woodbury, New York: American Institute of Physics.

Collier, J. D. 2002. Private communication.

Conrad, M. 1983. Adaptability: the Significance of Variability from Molecule to Ecosystem. New York: Plenum Press.

Cottam, R.; Ranson, W.; and Vounckx, R., 1997a. Localisation and Nonlocality in Computation. Holcombe, M., and Paton, R. C. eds. Information Processing in Cells and Tissues, 197-202. New York: Plenum Press.

Cottam, R.; Ranson, W.; Langloh, N.; and Vounckx, R. 1997b. A Unified Quasi-Particulate Framework for Evolution. Nehaniv, C. L. ed. Technical Report, 97-1-010, Mathematical and Computational Biology: Computational Morphogenesis, Hierarchical Complexity, and Digital Evolution, 29. The University of Aizu, Japan.

Cottam, R.; Ranson, W.; and Vounckx, R. 1998a. Emergence: Half a Quantum Jump? Acta Polytechnica Scandinavica 91:12-19.

Cottam, R.; Ranson, W.; and Vounckx, R. 1998b. Diffuse Rationality in Complex Systems. Interjournal of Complex Systems Article #235.

Cottam, R.; Ranson, W.; and Vounckx, R. 1998c. Consciousness: the Precursor to Life? In Proceedings of the Third German Workshop on Artificial Life, 239-248. Thun, Germany: Verlag Harri Deutsch.

Cottam, R.; Ranson, W.; and Vounckx, R. 1998d. Diffuse Rationality in Complex Systems. Proceedings of the Second International Conference on Complex Systems. Nashua, NH: NECSI. Forthcoming.

Cottam, R.; Ranson, W.; and Vounckx, R. 1999a. A Biologically-Consistent Diffuse Semiotic Architecture for Survivalist Information Processing. Proceedings of the Seventh World Congress of the International Association for Semiotic Studies: Sign Processes in Complex Systems. Technical University of Dresden, Germany. Forthcoming.

Cottam, R.; Ranson, W.; and Vounckx, R. 1999b. A Biologically Consistent Hierarchical Framework for Self-Referencing Survivalist Computation. In Proceedings of Computing Anticipatory Systems: CASYS'98 - 2nd International Conference, AIP Conference Proceedings 465, 252-262. Woodbury, New York: American Institute of Physics.

Cottam, R.; Ranson, W.; and Vounckx, R. 1999c. Life as Its Own Tool for Survival. In Proceedings of Forty-Third Annual Conference of the International Society for the Systems Science, #99-168, 1-12. Pacific Groove, CA: ISSS.

Cottam, R.; Ranson, W.; and Vounckx, R. 2000a. Executing Emergence! In Proceedings of the Fourth International Conference on Emergence, Complexity, Hierarchy and Order. Washington, DC: ISSE. Forthcoming.

Cottam, R.; Ranson, W.; and Vounckx, R. 2000b. A Diffuse Biosemiotic Model for Cell-to-Tissue Computational Closure. BioSystems 55:159-171.

Cottam, R.; Ranson, W.; and Vounckx, R., 2001b. Cross-scale, Richness, Cross-assembly, Logic 1, Logic 2, Pianos and Builders. Proceedings of the International Conference on the Integration of Information Processing. Toronto, Canada: SEE. Forthcoming.

Cottam, R.; Ranson, W.; and Vounckx, R., 2002a. Self-Organization and Complexity in Large Networked Information-processing Systems. Proceedings of the Fourth International Conference on Complex Systems. Nashua, NH: NECSI. Forthcoming.

Cottam, R.; Ranson, W.; and Vounckx, R., 2002b. Lifelike Robotic Collaboration Requires Lifelike Information Integration. Proceedings of the Performance Metrics for Intelligent Systems Workshop. Gaithersburg, MD: NIST. Forthcoming.

Dempster, A. P. 1967. Annals of Mathematical Statistics 38:325-339.

Edmonds, B. 1996. What is Complexity? The Philosophy of Complexity per se with Application to Some Examples in Evolution. Heylighen, F.; Bollen, J.; and Riegler, A. eds. The Evolution of Complexity: the Violet Book of ‘Einstein meets Magritte’ (V.8). Dordrecht: Kluwer Academic.

Farre, G. L. 2002. Human Cognition: a Quantal Property? In Proceedings of the Fourth International Conference on Emergence, Complexity, Hierarchy and Order. Washington, DC: ISSE. Forthcoming.

Green, M. B.; Schwarz, J. H.; and Witten, E. 1987. Superstring Theory, Volume I, 184. Cambridge: Cambridge U. P.

Haken, H. 1984. The Science of Structure: Synergetics. New York: Prentice Hall.

Hawking, S. W. 1975. Black Holes are White Hot. Annals of the New York Academy of Sciences 262:289.

Hoffmeyer, J.; and Emmeche, C. 1991a. From Language to Nature – the Semiotic Metaphor in Biology. Semiotica 84:1-42.

Hoffmeyer, J.; and Emmeche, C. 1991a. Code-Duality and the Semiotics of Nature. Anderson, M., and Merrell, F. eds. On Semiotic Modeling, 117-166. Berlin and New York: Mouton de Gruyter.

Langloh, N.; Cottam, R.; Vounckx, R.; and Cornelis, J. 1993. Towards Distributed Statistical Processing: A Query and Reflection Interaction Using Magic: Mathematical Algorithms Generating Interdependent Confidences. Smith, S. D. and Neale, R. F. eds. Optical Information Technology, 303-319. Berlin, Germany: Springer-Verlag.

LeDoux, J. E. 1992. Brain Mechanisms of Emotion and Emotional Learning. Curr. Opin. Neurobiology 2: 191-197.

Matsuno, K. 1996. Internalist Stance and the Physics of Information. BioSystems 38:111-118.

Matsuno, K. 2000. Is There a Biology of Quantum Information? BioSystems 55: 39-46.

Matsuno, K. 2002. Quantum Mechanics in First, Second and Third Person Descriptions. BioSystems. Forthcoming.

Mikulecky, D. 1999. Definition of Complexity. http://views.vcu.edu/~mikuleck/ON%20COMPLEXITY.html

Pribram, K. H. 1991. Brain and Perception: Holonomy and Structure in Figural Processing. Hillsdale, NJ: Lawrence Erlbaum.

Pribram, K. H. 2001. Proposal for a Quantum Physical Basis for Selective Learning. In Proceedings of the Fourth International Conference on Emergence, Complexity, Hierarchy and Order. Washington, DC: ISSE. Forthcoming.

Root-Bernstein, R. S.; and Dillon, P. F. 1997. Molecular Complementarity I: the Complementarity Theory of the Origin and Evolution of Life. Journal of Theoretical Biology 188:447-479.

Rosen, R. 1985. Anticipatory Systems. New York: Pergamon Press.

Schempp, W. 1992. Quantum Holography and Neurocomputer Architectures. Journal of Mathematical Imaging and Vision 2:279-326.

Schempp, W. 2000. Quantum Entanglement and Relativity. In Proceedings of the Fourth International Conference on Emergence, Complexity, Hierarchy and Order. Washington, DC: ISSE. Forthcoming.

Schempp, W. 2001. Private communication.

Shafer, G. A. 1976. Mathematical Theory of Evidence. Princeton: U. P.

Taborsky, E. 1998. Architectonics of Semiosis (Semaphores and Signs). London: Macmillan.

Taborsky, E. 1999. Private communication.

Taborsky, E. 2002. Semiosis and Energy Transformation. International Journal of Computing Anticipatory Systems. Forthcoming.

Tononi, G.; and Edelman, G. M. 1998. Consciousness and Complexity. Science 282:1846-1851.

Endnotes